Основания трапеции равны \(\displaystyle 18\) и \(\displaystyle 6\small,\) боковая сторона, равная \(\displaystyle 7\small,\) образует с одним из оснований трапеции угол \(\displaystyle 150^\circ\small.\) Найдите площадь трапеции.
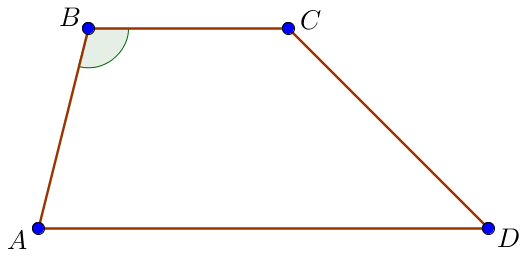
Пусть \(\displaystyle AD=18\) и \(\displaystyle BC=6\) – основания, \(\displaystyle AB=7\) – боковая сторона трапеции \(\displaystyle ABCD\small.\) Требуется найти площадь трапеции.
Найдем высоту трапеции. Возможны два варианта: \(\displaystyle \angle ABC = 150^{\circ}\) и \(\displaystyle \ \angle BAD= 150^{\circ}\small.\)
По предложенному в условии задачи рисунку имеем \(\displaystyle \angle ABC = 150^{\circ}\small.\) Так как сумма углов при боковой стороне трапеции равна \(\displaystyle 180^{\circ}\small,\) то \(\displaystyle \angle BAD = 180^{\circ}-\angle ABC =\) \(\displaystyle =180^{\circ}-150^{\circ}=30^{\circ}\small.\) Проведем высоту \(\displaystyle BH \) трапеции. | 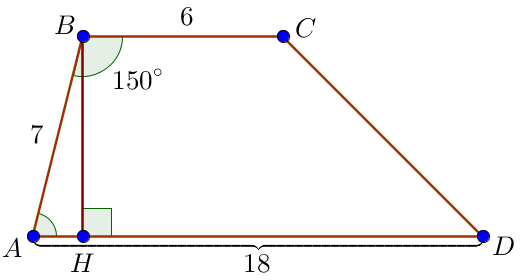 |
Найдем высоту \(\displaystyle BH \) из прямоугольного треугольника \(\displaystyle ABH\small.\) Нам известны острый угол \(\displaystyle \angle BAH=30^{\circ}\) и гипотенуза \(\displaystyle AB=7\small.\) По свойству прямоугольного треугольника с острым углом \(\displaystyle 30^{\circ}\small,\) катет, лежащий против угла \(\displaystyle 30^{\circ}\small,\) равен половине гипотенузы. Тогда \(\displaystyle BH=\frac{1}{2}\cdot {AB}=\frac{1}{2}\cdot 7=3{,}5\small.\) | 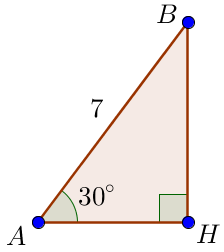 |
Так как площадь трапеции равна произведению полусуммы оснований на высоту, то
\(\displaystyle S_{ABCD}=\frac{AD+BC}{2}\cdot BH=\frac{18+6}{2}\cdot 3{,}5=\frac{24}{2}\cdot 3{,}5={12}\cdot 3{,}5=42\small.\)
Ответ: \(\displaystyle 42 \small.\)
Рассмотрим случай \(\displaystyle \angle BAD= 150^{\circ} \small.\) Так как сумма углов при боковой стороне трапеции равна \(\displaystyle 180^{\circ}\small,\) то \(\displaystyle \angle ABC = 180^{\circ}-\angle BAD =\) \(\displaystyle =180^{\circ}-150^{\circ}=30^{\circ} \small.\) Проведем высоту \(\displaystyle AH \) трапеции. | 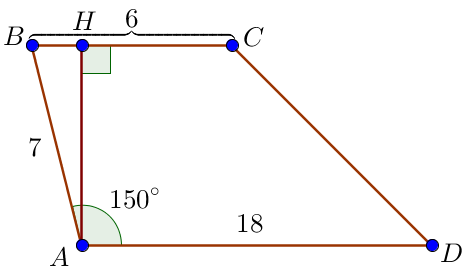 |
Получаем прямоугольный треугольник \(\displaystyle ABH\) с острым углом \(\displaystyle \angle ABH =30^{\circ}\) и гипотенузой \(\displaystyle AB=7 \small.\) По свойству прямоугольного треугольника с острым углом \(\displaystyle 30^{\circ} \small,\) катет, лежащий против угла \(\displaystyle 30^{\circ} \small,\) равен половине гипотенузы. Значит, \(\displaystyle AH=\frac{1}{2}\cdot {AB}=\frac{1}{2}\cdot 7=3{,}5 \small.\) Площадь трапеции и в этом случае равна \(\displaystyle 42 \small.\) | 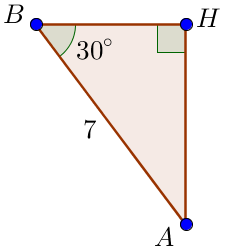 |