Найдите площадь ромба, если его высота равна \(\displaystyle 2 \small,\) а синус острого угла равен \(\displaystyle 0{,}2 \small.\)
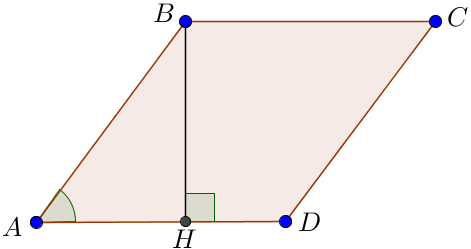

Пусть \(\displaystyle a\) – сторона ромба.
Воспользуемся формулой для вычисления площади ромба
\(\displaystyle S=a^2 \cdot \sin \alpha \small,\)
где \(\displaystyle \alpha \) – угол между сторонами ромба.
В данном случае \(\displaystyle \sin \alpha =0{,}2 \small,\) поэтому
\(\displaystyle S=a^2 \cdot 0{,}2 {\small .}\)
Воспользуемся другой формулой для вычисления площади ромба
\(\displaystyle S=h\cdot a \small,\)
где \(\displaystyle h\) – высота ромба.
В данном случае \(\displaystyle h =2 \small, \) поэтому
\(\displaystyle {S} = {2 }\cdot a {\small.}\)
Из двух соотношений
\(\displaystyle S=a^2 \cdot 0{,}2 {\small. }\)
и
\(\displaystyle {S} = {2 }\cdot a {\small. }\)
получаем уравнение
\(\displaystyle a^2 \cdot 0{,}2 = {2 }\cdot a {\small.}\)
Поскольку длина отрезка не равна нулю, можно разделить обе части равенства на \(\displaystyle 0{,}2a {\small.}\)
\(\displaystyle a^2 \cdot 0{,}2 = {2 }\cdot a \, \bigg| :\color{red}{0{,}2 a}{\small ,}\)
\(\displaystyle a = {10 } {\small.}\)
Тогда
\(\displaystyle S=h\cdot a = 2\cdot 10 = 20 \small.\)
Ответ: \(\displaystyle 20 {\small .}\)