Задание
Найдите сторону ромба, высота которого в \(\displaystyle {3}\) раза меньше стороны, а площадь равна \(\displaystyle 12 \small.\)
Решение
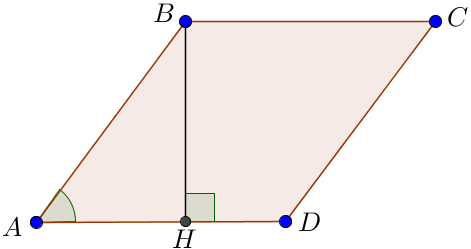
Пусть \(\displaystyle BH=x\) – высота ромба, тогда \(\displaystyle AD=3x \) – сторона ромба.
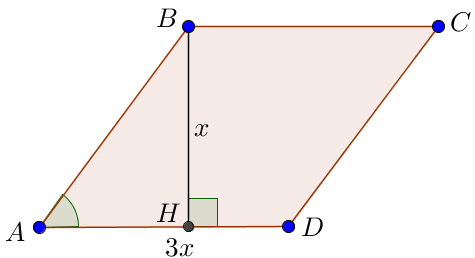
Поскольку площадь ромба равна произведению высоты на основание
\(\displaystyle {S_{ромб}} = {BH }\cdot AD \small,\)
то
\(\displaystyle 12 = x \cdot 3x {\small .}\)
Получаем:
\(\displaystyle 12 = 3 \cdot x^2{\small,}\)
\(\displaystyle x^2=4{\small .}\)
Поскольку длина отрезка положительна, то \(\displaystyle x = \sqrt{4}=2 {\small .}\)
Тогда \(\displaystyle AD=3x=6 \small. \)
Ответ: \(\displaystyle 6 {\small .}\)