В прямоугольном треугольнике \(\displaystyle ABC\) угол между биссектрисой \(\displaystyle CD\) и медианой \(\displaystyle CM{\small , }\) проведенными из вершины прямого угла, равен \(\displaystyle 14^\circ{\small .}\) Найдите больший из острых углов прямоугольного треугольника \(\displaystyle ABC{\small .}\)
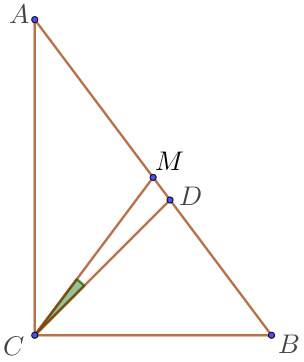
Так как медиана, проведенная к гипотенузе, равна половине гипотенузы, то треугольники \(\displaystyle AMC \) и \(\displaystyle CMB \) – равнобедренные.
Пусть \(\displaystyle \angle B= \alpha{\small .} \) Так как \(\displaystyle \triangle CMB \) – равнобедренный, то \(\displaystyle \angle MCB= \angle B= \alpha{\small :} \)
Так как \(\displaystyle CD \) – биссектриса, то \(\displaystyle \angle BCD= 45^\circ{\small .} \)
В целом имеем:
Тогда
\(\displaystyle \angle MCB= \angle MCD+ \angle DCB{\small , } \)
\(\displaystyle \alpha= 14^\circ+ 45^\circ{\small , } \)
\(\displaystyle \alpha= 59^\circ{\small , } \)
\(\displaystyle \angle B= 59^\circ{\small . } \)
Так как \(\displaystyle \angle A+ \angle B= 90^\circ{\small , } \) то \(\displaystyle \angle A= 90^\circ- 59^\circ= 21^\circ{\small .} \)
Наибольший острый угол равен \(\displaystyle 59^\circ{\small .} \)
Ответ: \(\displaystyle 59 {\small .} \)