Skip to main content

Теория: 08 Площадь поверхности пирамиды

Задание

Сторона основания правильной четырехугольной пирамиды равна \(\displaystyle 4{\small ,}\) а площадь поверхности пирамиды равна \(\displaystyle 64{\small .}\) Найдите апофему. 

Решение

Воспользуемся определением.

Определение

Апофема правильной пирамиды

Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.

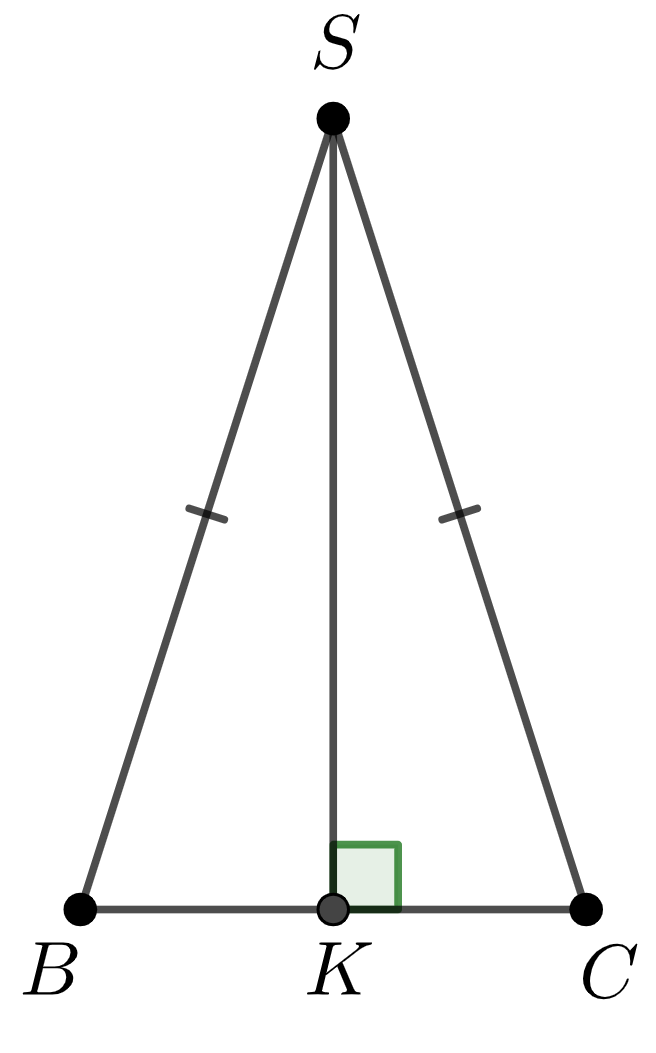
Тогда \(\displaystyle SK\) – апофема данной пирамиды.

Пусть \(\displaystyle BC=4\) – сторона основания правильной треугольной пирамиды.

В условии задачи дана площадь поверхности пирамиды. 

Воспользуемся формулой для вычисления площади полной поверхности пирамиды.

Правило

Площадь полной поверхности пирамиды

Площадь полной поверхности пирамиды \(\displaystyle S \) равна

\(\displaystyle S=S_{осн}+S_{бок} { \small ,} \)

где \(\displaystyle S_{осн} \) – площадь основания,

\(\displaystyle S_{бок}\) – площадь боковой поверхности пирамиды.

\(\displaystyle S_{осн}=16\)

\(\displaystyle S_{бок}=8 \cdot SK \)

Подставим \(\displaystyle S_{осн}\) и \(\displaystyle S_{бок}\)​ в формулу площади полной поверхности пирамиды:

\(\displaystyle S=S_{осн}+S_{бок} {\small ,}\)

\(\displaystyle S=16+8\cdot SK {\small .}\)

Подставим \(\displaystyle S\) и вычислим апофему пирамиды \(\displaystyle SK{\small :}\)

\(\displaystyle 64=16+8\cdot SK{ \small ,} \)

\(\displaystyle 8\cdot SK=48{ \small ,}\)

\(\displaystyle SK=6{ \small .}\)

Ответ: \(\displaystyle 6{\small .}\)