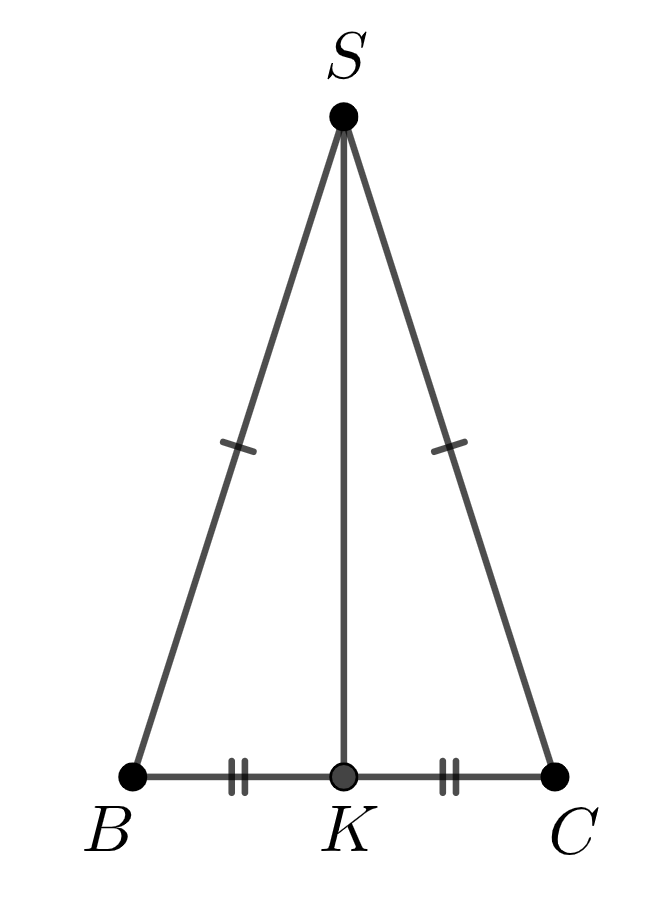
В правильной треугольной пирамиде \(\displaystyle SABC\) точка \(\displaystyle K\) – середина ребра \(\displaystyle BC{\small ,}\) \(\displaystyle S\) – вершина. Известно, что \(\displaystyle SK = 4{\small ,}\) а \(\displaystyle AC=9{\small .}\) Найдите площадь боковой поверхности пирамиды.
Способ 1
Требуется найти площадь боковой поверхности \(\displaystyle S_{бок}\) правильной пирамиды. Эта площадь равна сумме площадей всех боковых граней.
Боковые грани правильной пирамиды – равные треугольники. Следовательно, площади боковых граней равны.
У правильной треугольной пирамиды три боковых грани. Значит,
\(\displaystyle S_{бок}=S_{грани}+S_{грани}+S_{грани}=3S_{грани}\small. \)
Вычислим \(\displaystyle S_{грани}\small. \)
Получаем:
\(\displaystyle S_{бок}=3 \cdot S_{грани}=3\cdot 18 = 54\small. \)
Способ 2
Воспользуемся формулой для вычисления площади боковой поверхности пирамиды.
Площадь боковой поверхности правильной пирамиды
Площадь боковой поверхности правильной пирамиды \(\displaystyle S_{бок} \) равна половине произведения периметра основания на апофему.
\(\displaystyle S_{бок}=\frac{1}{2}P_{осн} \cdot l{ \small ,} \)
где \(\displaystyle P_{осн} \) – периметр основания,
\(\displaystyle l\) – апофема.
Периметр основания правильной треугольной пирамиды равен
\(\displaystyle P_{осн}=3\cdot AC{\small .}\)
Подставим найденные значения \(\displaystyle P_{осн}\) и \(\displaystyle l\) в формулу для \(\displaystyle S_{бок}{\small :}\)
\(\displaystyle S_{бок}=\frac{1}{2}P_{осн} \cdot l{ \small ,} \)
\(\displaystyle S_{бок}=\frac{1}{2}\cdot 3 \cdot AC \cdot SK{ \small .} \)
Подставим значения \(\displaystyle AC\) и \(\displaystyle SK{\small :}\)
\(\displaystyle S_{бок}=\frac{1}{2}\cdot 3 \cdot 9 \cdot 4=54{ \small .}\)
Ответ: \(\displaystyle 54{\small .}\)