План местности разбит на клетки. Каждая клетка обозначает квадрат \(\displaystyle 1 {\small м}\times 1 {\small м} {\small.}\) Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
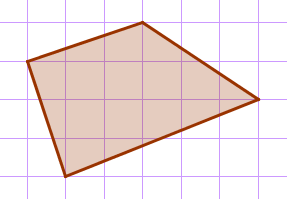
| Дополним исходную фигуру (участок) прямоугольными треугольниками так, чтобы можно было легко вычислить площадь новой построенной фигуры. Получаем прямоугольник со сторонами \(\displaystyle 4\, {\small м} \) и \(\displaystyle 6 {\,\small м .}\) | 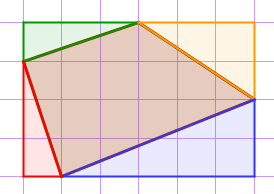 |
Площадь участка равна площади прямоугольника без площадей достроенных треугольников.
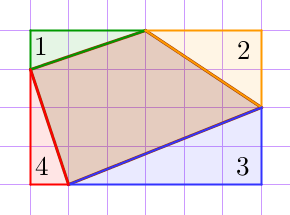 | Площадь прямоугольника равна \(\displaystyle 4\cdot 6=24\, {\small м^2. }\) Площадь первого треугольника равна \(\displaystyle \frac{1}{2}\cdot 1\cdot 3=1{,}5\, {\small м^2 ; }\) площадь второго треугольника равна \(\displaystyle \frac{1}{2}\cdot 3\cdot 2=3\, {\small м^2; }\) площадь третьего треугольника равна \(\displaystyle \frac{1}{2}\cdot 2\cdot 5=5 \, {\small м^2; }\) площадь четвертого треугольника равна \(\displaystyle \frac{1}{2}\cdot 1\cdot 3=1{,}5\, {\small м^2. }\) |
Такими образом, площадь участка равна
\(\displaystyle 24- 1{,}5 -3 -5-1{,}5=13 \, \small м^2. \)
Ответ: \(\displaystyle 13{\small . }\)