Найдите острый угол параллелограмма со сторонами \(\displaystyle 5\) и \(\displaystyle 4\) и площадью \(\displaystyle 10 \small.\)
Пусть стороны параллелограмма \(\displaystyle AB=4\) и \(\displaystyle AD=5 \small,\) \(\displaystyle \angle BAD\) – острый угол параллелограмма.
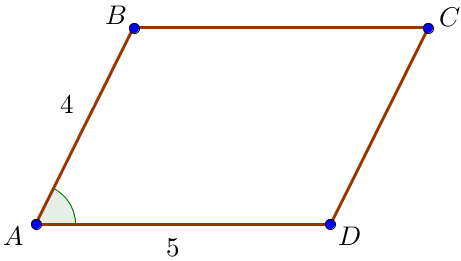
Площадь параллелограмма может быть найдена как произведение смежных сторон на синус угла между ними:
\(\displaystyle {S_{пар}} = {AB}\cdot AD \cdot \sin \angle BAD {\small.}\)
Подставим данные значения в формулу для вычисления площади параллелограмма:
\(\displaystyle 10 = 4\cdot 5 \cdot \sin \angle BAD {\small ,}\)
\(\displaystyle 10 = 20 \cdot \sin \angle BAD {\small ,}\)
\(\displaystyle \sin \angle BAD =\frac{1}{2}{\small.}\)
Поскольку \(\displaystyle \angle BAD \) – острый, то \(\displaystyle \angle BAD =30^{\circ} {\small.}\)
Ответ: \(\displaystyle 30^{\circ} {\small .}\)