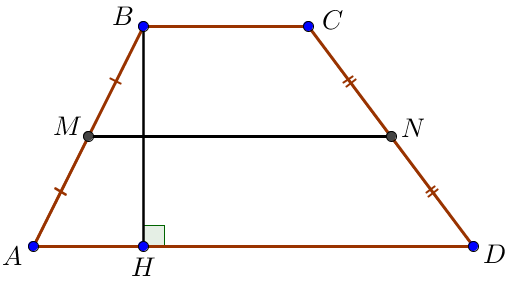
В трапеции \(\displaystyle ABCD\) с основаниями \(\displaystyle AD=16\) и \(\displaystyle BC=12\) провели среднюю линию \(\displaystyle MN\small.\) Найдите высоту трапеции, если площадь четырехугольника \(\displaystyle AMND\) равна \(\displaystyle 75\small.\)
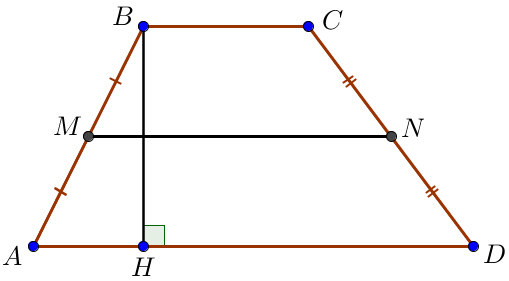
Так как средняя линия трапеции равна полусумме оснований, то \(\displaystyle MN=\frac{AD+BC}{2}=\frac{16+12}{2}=\frac{28}{2}=14\small.\) Рассмотрим четырехугольник \(\displaystyle AMND\small.\\ \) В нем стороны \(\displaystyle MN\) и \(\displaystyle AD\) параллельны по свойству средней линии трапеции. Прямые \(\displaystyle AM\) и \(\displaystyle DN\) не параллельны, так как содержат боковые стороны исходной трапеции. Значит, четырехугольник \(\displaystyle AMND\) является трапецией. | 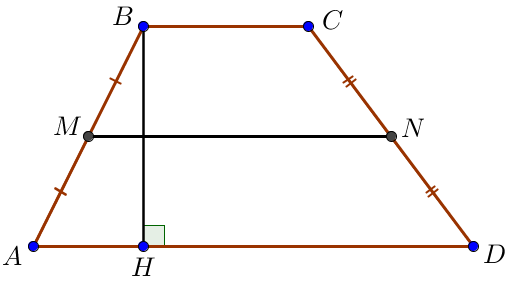 |
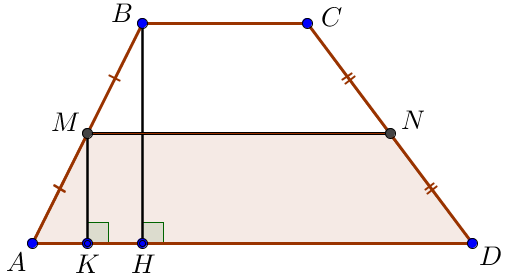
Пусть \(\displaystyle BH\) – высота трапеции \(\displaystyle ABCD\small.\)
Рассмотрим треугольник \(\displaystyle ABH\small.\) Обозначим через \(\displaystyle K\) середину отрезка \(\displaystyle AH\small.\) Тогда \(\displaystyle MK\) является средней линией \(\displaystyle ABH\small.\) По свойству средней линии треугольника:
| 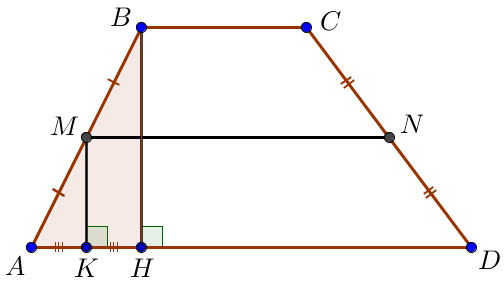 |
Следовательно, \(\displaystyle MK\) является высотой трапеции \(\displaystyle AMND\small.\)
Так как
\(\displaystyle S_{AMND}=\frac{AD+MN}{2}\cdot MK\)
и
\(\displaystyle S_{AMND}=75\small,\)
то получаем
\(\displaystyle \frac{AD+MN}{2}\cdot MK=75\small,\)
откуда
\(\displaystyle \frac{16+14}{2}\cdot MK=75\small,\)
\(\displaystyle \frac{30}{2}\cdot MK=75\small,\)
\(\displaystyle 15\cdot MK=75\small,\)
\(\displaystyle MK=\frac{75}{15}=5\small.\)
Тогда
\(\displaystyle BH=MK\cdot 2=5\cdot 2=10\small.\)
Ответ: \(\displaystyle 10{\small .}\)