В трапеции \(\displaystyle ABCD\) с основаниями \(\displaystyle AD=16\) и \(\displaystyle BC=12\) провели среднюю линию \(\displaystyle MN\small.\) Найдите расстояние между серединами отрезков \(\displaystyle MB\) и \(\displaystyle CN\small.\)
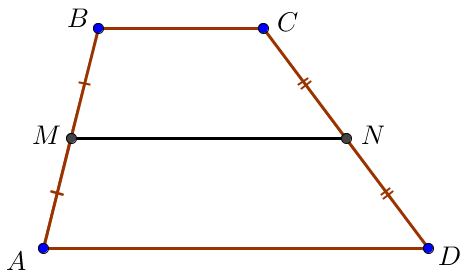
Так как средняя линия трапеции равна полусумме оснований, то
\(\displaystyle MN=\frac{AD+BC}{2}=\frac{16+12}{2}=\frac{28}{2}=14\small.\)
Воспользуемся свойством средней линии трапеции.
Средняя линия трапеции параллельна основаниям трапеции.
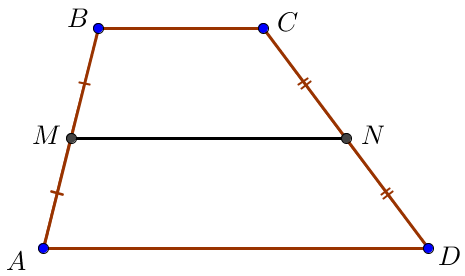
\(\displaystyle MN\parallel BC\parallel AD\)
Тогда в четырехугольнике \(\displaystyle MBCN\) стороны \(\displaystyle MN\) и \(\displaystyle BC\) параллельны, а прямые \(\displaystyle MB\) и \(\displaystyle NC\) не параллельны, так как содержат боковые стороны исходной трапеции.
Значит, четырехугольник \(\displaystyle MBCN\) является трапецией.
В задаче требуется найти среднюю линию \(\displaystyle m\) трапеции \(\displaystyle MBCN\small.\)
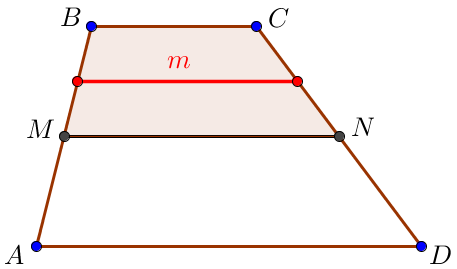
Так как средняя линия трапеции равна полусумме оснований, то
\(\displaystyle m=\frac{MN+BC}{2}=\frac{14+12}{2}=\frac{26}{2}=13\small.\)
Ответ: \(\displaystyle 13{\small .}\)