Высота, опущенная из вершины тупого угла на большее основание равнобедренной трапеции, делит его на отрезки, равные \(\displaystyle 10\) и \(\displaystyle 4\small.\) Найдите среднюю линию этой трапеции.
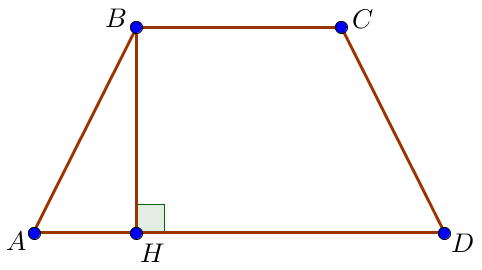
Пусть \(\displaystyle BC\) – меньшее, а \(\displaystyle AD\) – большее основания трапеции, \(\displaystyle BH_1\) и \(\displaystyle CH_2\) – высоты трапеции. Пусть высота \(\displaystyle BH_1\) делит основание \(\displaystyle AD\) на отрезки \(\displaystyle AH_1=4\) и \(\displaystyle H_1D=10\small.\) Получаем: \(\displaystyle AD=AH_1+H_1D=\) \(\displaystyle =4+10=14\small.\) | 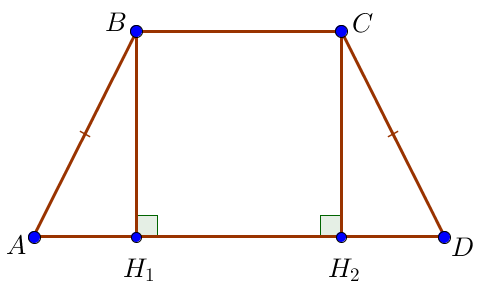 |
Прямоугольные треугольники \(\displaystyle ABH_1\) и \(\displaystyle DCH_2\) равны по гипотенузе \(\displaystyle AB=CD\) и катету \(\displaystyle BH_1=CH_2\small.\) Тогда \(\displaystyle DH_2=AH_1=4\) \(\displaystyle H_1H_2=10-4=6\small.\) | 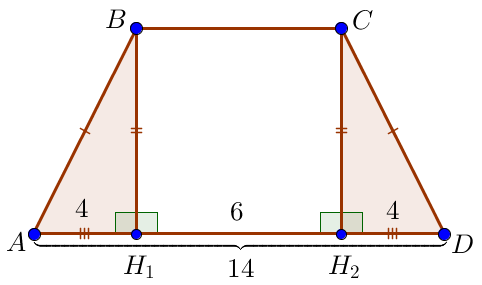 |
В четырехугольнике \(\displaystyle H_1BCH_2\) все углы прямые. Значит, он является прямоугольником. Следовательно,
\(\displaystyle BC=H_1H_2=6\small.\)
По свойству средней линии трапеции,
\(\displaystyle m=\frac{BC+AD}{2}\small,\)
где \(\displaystyle m\) – средняя линия трапеции. Тогда
\(\displaystyle m=\frac{BC+AD}{2}=\frac{6+14}{2}=\frac{20}{2}=10\small.\)
Ответ: \(\displaystyle 10{\small .}\)