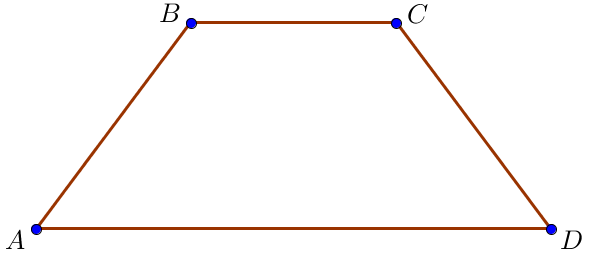
Основания равнобедренной трапеции равны \(\displaystyle 9\) и \(\displaystyle 21\small,\) а её боковые стороны равны \(\displaystyle 10\small.\) Найдите диагональ трапеции.
Пусть \(\displaystyle AD=21\) и \(\displaystyle BC=9\) – основания, \(\displaystyle AB=CD=10\) – боковые стороны, \(\displaystyle BH \) и \(\displaystyle CK \) – высоты трапеции \(\displaystyle ABCD\small.\) Поскольку основания трапеции параллельны, а высоты трапеции перпендикулярны основаниям, \(\displaystyle BH K C \) – прямоугольник. Тогда \(\displaystyle H K = BC= 9\small .\) | 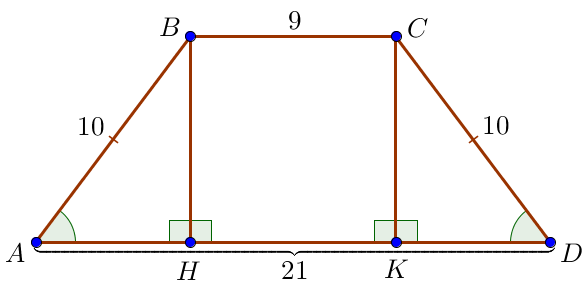 |
Прямоугольные треугольники \(\displaystyle ABH\) и \(\displaystyle DCK\) равны по гипотенузе \(\displaystyle AB=CD\) и катету \(\displaystyle BH=CK\small.\) Значит \(\displaystyle AH=DK\) и \(\displaystyle \begin{aligned} AH&=DK=\frac{AD-BC}{2}=\\ \\ &=\frac{21-9}{2}=\frac{12}{2}=6\small. \end{aligned}\) | 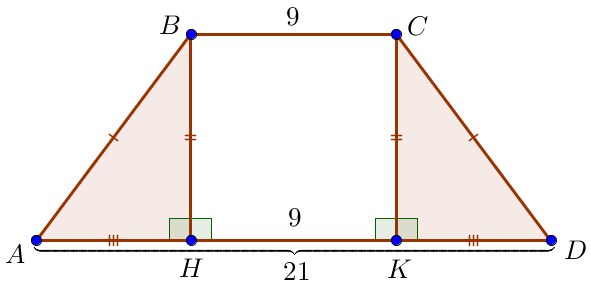 |
Рассмотрим прямоугольный треугольник \(\displaystyle ABH \small.\) Найдем высоту \(\displaystyle BH\) трапеции. По теореме Пифагора \(\displaystyle BH^2=AB^2-AH^2\small.\) Значит, \(\displaystyle BH^2=10^2-6^2=100-36=64=8^2\small.\) Поскольку длина отрезка положительна, то \(\displaystyle BH=8\small.\) | 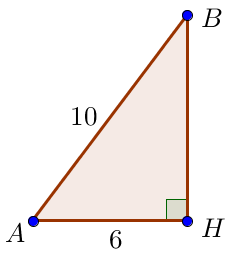 |
Рассмотрим прямоугольный треугольник \(\displaystyle BHD \small.\) Нам известны его катеты \(\displaystyle BH=8\) и \(\displaystyle DH=DK+HK=6+9=15\small.\) Найдем диагональ \(\displaystyle BD\) трапеции. По теореме Пифагора \(\displaystyle \begin{aligned}BD^2&=BH^2+DH^2=\\&=8^2+15^2=64+225=289=17^2\small.\end{aligned}\) Поскольку длина отрезка положительна, то \(\displaystyle BD=17\small.\) | 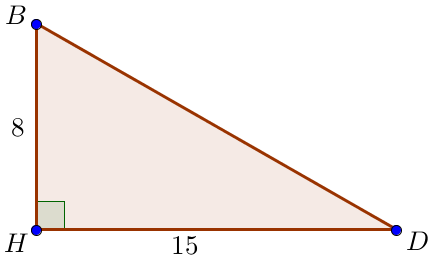 |
Ответ: \(\displaystyle 17{\small .}\)