В равнобедренной трапеции \(\displaystyle ABCD\) с основаниями \(\displaystyle AD\) и \(\displaystyle BC\) \(\displaystyle O\) – точка пересечения диагоналей, \(\displaystyle BD=12\small,\) \(\displaystyle OC=5\small,\) \(\displaystyle \angle CAD=30^\circ\small.\) Найдите расстояние от точки \(\displaystyle O\) до прямой \(\displaystyle AD\small.\)
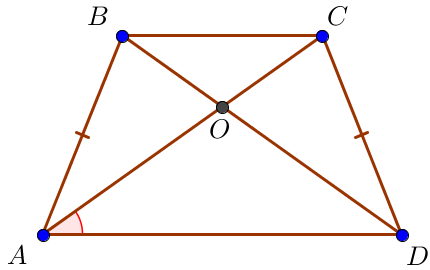
Воспользуемся свойством равнобедренной трапеции.
Свойство равнобедренной трапеции
Диагонали равнобедренной трапеции равны.
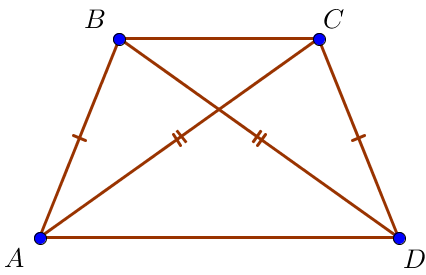
\(\displaystyle AC=BD\)
Значит,
\(\displaystyle AC=BD=12\small,\)
\(\displaystyle AO=AC-OC=12-5=7\small.\)
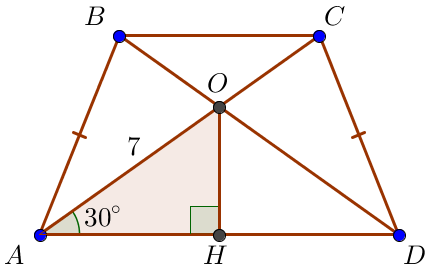
Пусть \(\displaystyle H\) – основание перпендикуляра, опущенного из точки \(\displaystyle O\) на \(\displaystyle AD\small.\) Длина отрезка \(\displaystyle OH\) равна расстоянию от точки \(\displaystyle O\) до прямой \(\displaystyle AD\small. \) Рассмотрим прямоугольный треугольник \(\displaystyle AOH\small.\) В прямоугольном треугольнике катет, лежащий против угла \(\displaystyle 30^{\circ}\small,\) равен половине гипотенузы. Тогда \(\displaystyle OH=\frac{1}{2}\cdot {AO}=\frac{1}{2}\cdot 7=3{,}5\small.\)
|  |
Ответ: \(\displaystyle 3{,}5 {\small .}\)