В трапеции \(\displaystyle ABCD\) известны основания \(\displaystyle AD=17\) и \(\displaystyle BC=3\small,\) боковая сторона \(\displaystyle AB=8\sqrt{2}\) и угол \(\displaystyle \angle BAD=45^{\circ}\small.\) Найдите боковую сторону \(\displaystyle CD\) трапеции.
Проведем высоты \(\displaystyle BH=CK\) трапеции. Поскольку основания трапеции параллельны, а высоты трапеции перпендикулярны основаниям, \(\displaystyle BH K C \) – прямоугольник. Тогда \(\displaystyle H K = BC= 3\small .\) | 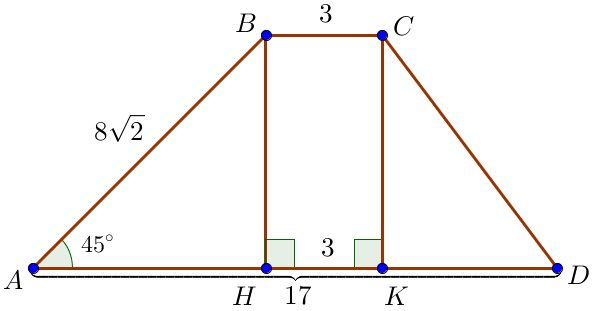 |
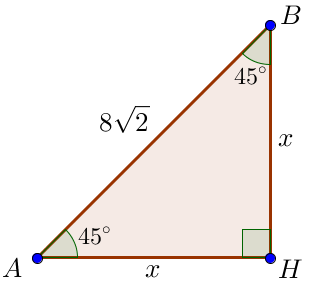
Рассмотрим прямоугольный треугольник \(\displaystyle ABH\small.\)
Нам известны острый угол \(\displaystyle \angle BAH=45^{\circ}\) и гипотенуза \(\displaystyle AB=8\sqrt{2}\small.\) Тогда
\(\displaystyle \angle ABH=180^{\circ}-\angle BAH-\angle AHB=180^{\circ}-45^{\circ}-90^{\circ}=45^{\circ}\small.\)
Так как \(\displaystyle \angle ABH=\angle BAH\small,\) то треугольник \(\displaystyle ABH\) равнобедренный, \(\displaystyle AH=BH\small.\)
Получили \(\displaystyle AH=BH=8\small.\)
Тогда \(\displaystyle KD=AD-AH-HK=17-8-3=6\small.\)
Рассмотрим прямоугольный треугольник \(\displaystyle DCK\small.\) Нам известны \(\displaystyle CK=8\) и \(\displaystyle DK=6\small.\) По теореме Пифагора \(\displaystyle CD^2=CK^2+DK^2=\) \(\displaystyle =8^2+6^2=64+36=100=10^2\small.\) Поскольку длина отрезка положительна, то \(\displaystyle CD=10\small.\) | 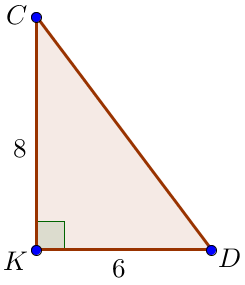 |
Ответ: \(\displaystyle 10 \small.\)