Выберите график прямой, заданной уравнением \(\displaystyle y=-\frac{8}{9}x-4\frac{1}{12}{\small , }\) исходя из знаков коэффициентов:
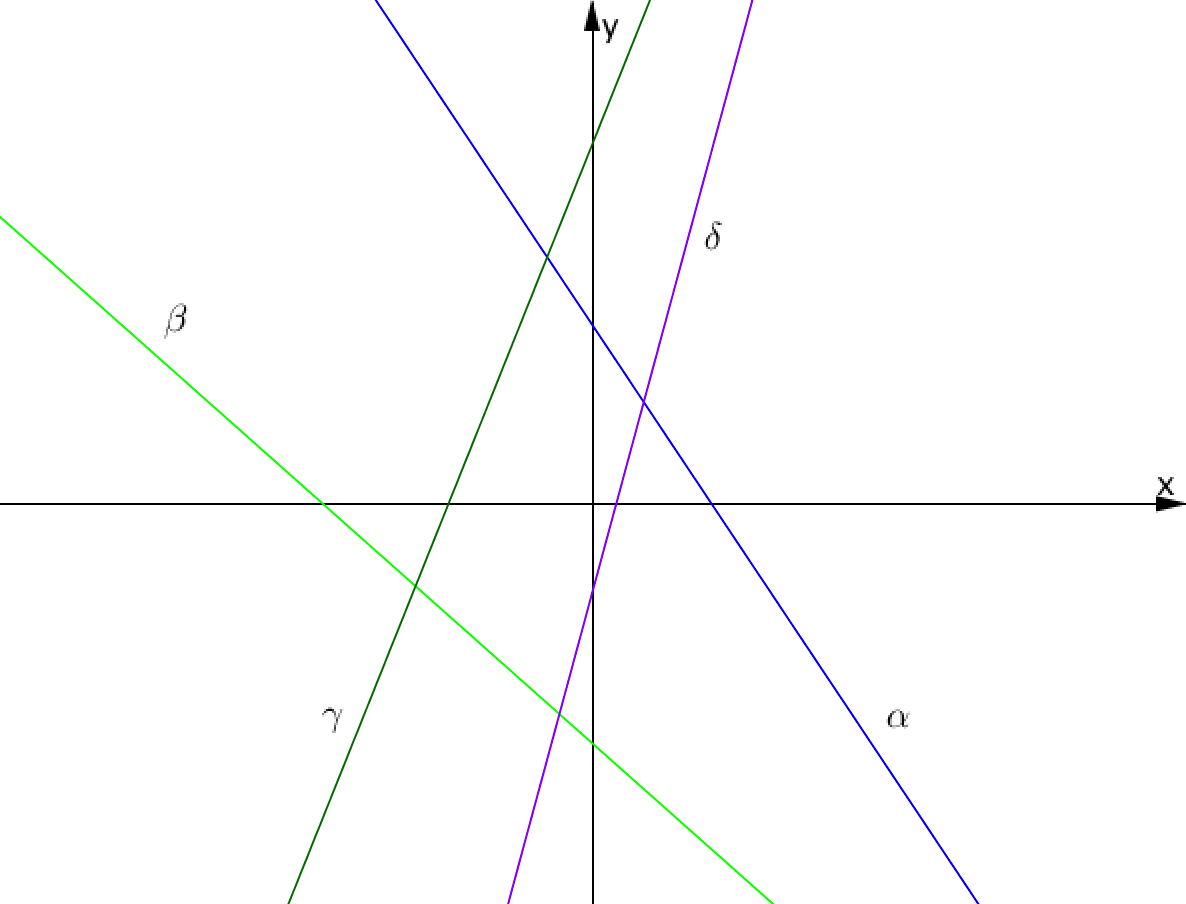
Сначала оценим в данной нам прямой \(\displaystyle y=-\frac{8}{9}x-4\frac{1}{12}\) знаки ее коэффициентов:
\(\displaystyle k=-\frac{8}{9}<0{\small ; } \)
\(\displaystyle b=-4\frac{1}{12}<0{\small . } \)
Значит, мы должны выбрать на рисунке такую прямую, у которой \(\displaystyle k<0 \) и \(\displaystyle b<0{\small . } \)
Проверим по порядку данные нам прямые.
Данная прямая имеет коэффициенты \(\displaystyle k<0 \) и \(\displaystyle b<0{\small . } \)
Значит, эта прямая нам подходит.
Таким образом, график прямой, заданной уравнением \(\displaystyle y=-\frac{8}{9}x-4\frac{1}{12}{\small , }\) – это прямая \(\displaystyle \bf\beta{\small . }\)
Ответ: \(\displaystyle \bf\beta{\small . }\)