Выберите верное уравнение прямой по заданному положению этой прямой на плоскости:
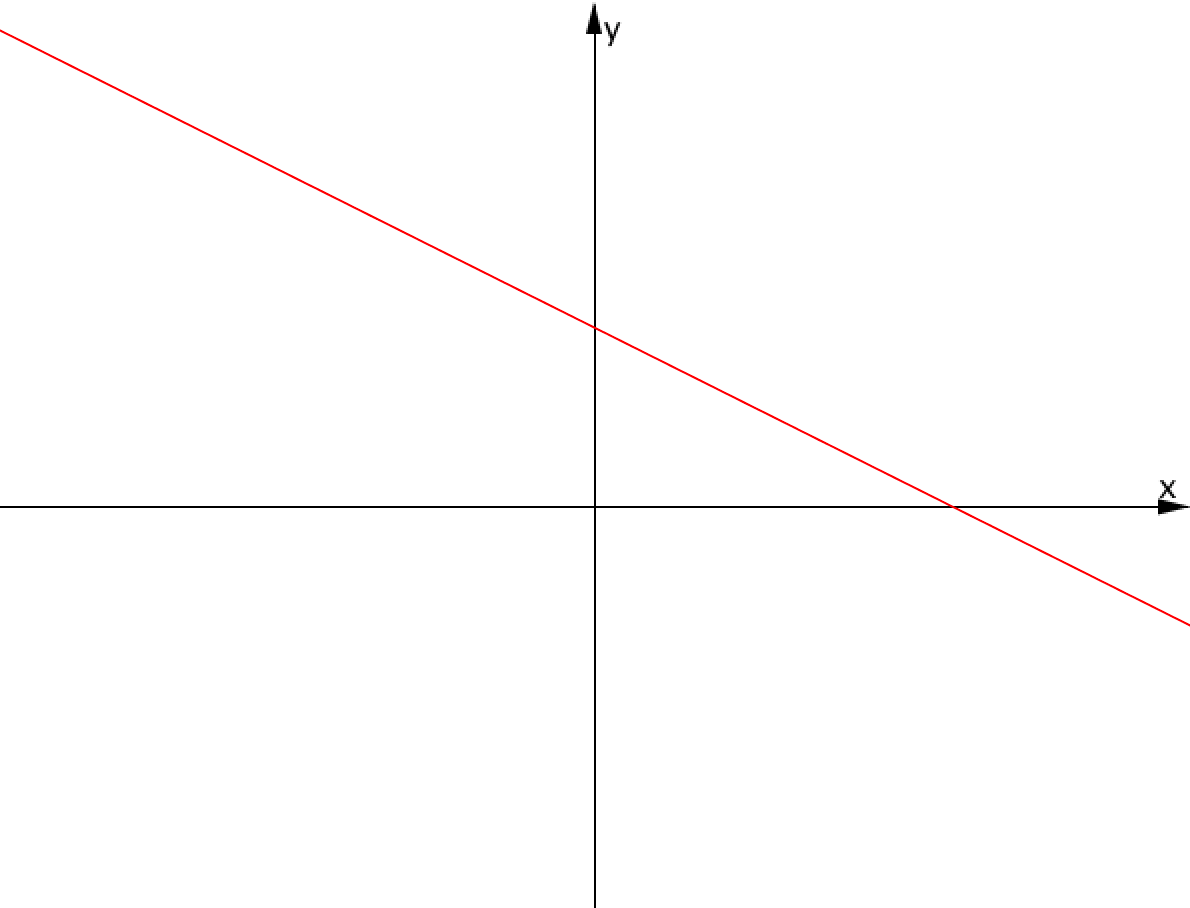
Данная прямая \(\displaystyle y=kx+b \) получена сдвигом на \(\displaystyle b \) единиц вверх прямой \(\displaystyle y=kx\,{\small :} \)
Следовательно, \(\displaystyle {\bf b>0}{\small .}\)
Прямая \(\displaystyle y=kx \) расположена во \(\displaystyle \rm II \) и \(\displaystyle \rm IV \) координатных четвертях:
Следовательно, \(\displaystyle {\bf k<0} {\small .}\)
Поэтому в уравнении \(\displaystyle y=kx+b \) искомой прямой знаки коэффициентов \(\displaystyle k \) и \(\displaystyle b \) должны быть:
\(\displaystyle k<0 \) и \(\displaystyle b>0{\small . } \)
Теперь определим знаки коэффициентов в уравнениях, заданных в вариантах ответов:
|
Прямая \(\displaystyle y=kx+b \) | \(\displaystyle k\) | \(\displaystyle b\) | Результат |
| \(\displaystyle y=\frac{2}{3}x-\frac{1}{9}\) | \(\displaystyle k=\frac{2}{3}>0 \) | \(\displaystyle b=-\frac{1}{9}<0 \) | не подходит |
| \(\displaystyle y=-\frac{1}{2}x+3 \) | \(\displaystyle k=\color{blue}{ -\frac{1}{2}<0} \) | \(\displaystyle b=\color{blue}{ 3>0}\) | подходит |
| \(\displaystyle y=-\frac{3}{4}x-\frac{1}{2}\) | \(\displaystyle k=-\frac{3}{4}<0\) | \(\displaystyle b=-\frac{1}{2}<0\) | не подходит |
| \(\displaystyle y=1\frac{1}{3}x+\frac{1}{4}\) | \(\displaystyle k=1\frac{1}{3}>0\) | \(\displaystyle b=\frac{1}{4}>0\) | не подходит |
Ответ: \(\displaystyle y=\frac{2}{3}x-\frac{1}{9}{\small . }\)