Известно положение прямой \(\displaystyle y=kx+b\) на плоскости:
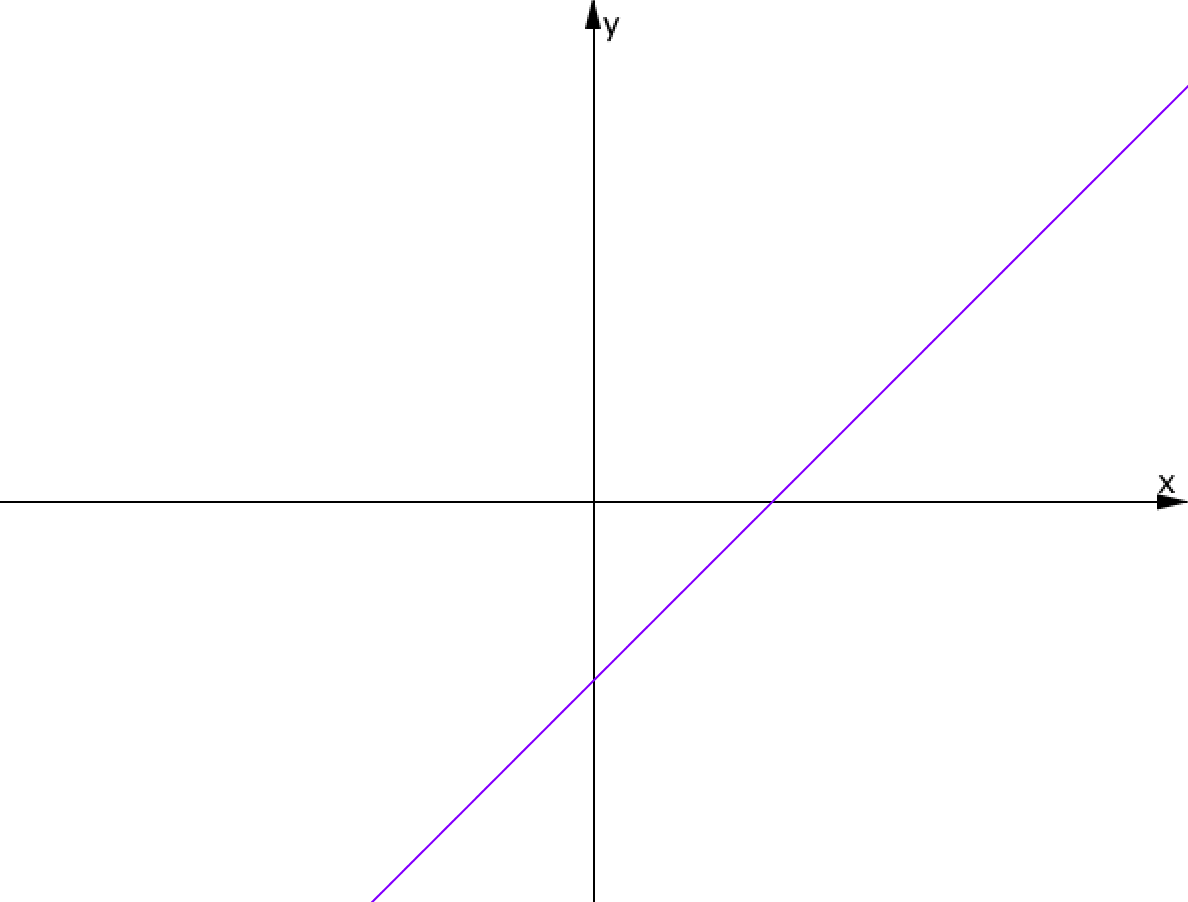
Определите знаки коэффициентов \(\displaystyle k\) и \(\displaystyle b\,{\small : }\)
\(\displaystyle k\) \(\displaystyle 0\)
\(\displaystyle b\) \(\displaystyle 0\)
Если отбросить коэффициент \(\displaystyle b{\small ,}\) то получится прямая \(\displaystyle y=kx{\small , } \) параллельная исходной прямой \(\displaystyle y=kx+b \) и проходящая через начало координат. Другими словами, прямая \(\displaystyle y=kx+b \) получена из прямой \(\displaystyle y=kx \) сдвигом на \(\displaystyle b \) единиц вниз:
Значит, \(\displaystyle \bf b<0{\small . } \)
Прямая \(\displaystyle y=kx \) лежит в \(\displaystyle \rm I \) и \(\displaystyle \rm III \) координатных четвертях:
Следовательно, ее коэффициент \(\displaystyle \bf k>0{\small . } \)
Таким образом, \(\displaystyle \bf k>0 \) и \(\displaystyle \bf b<0{\small . } \)