На рисунке изображены две прямые:
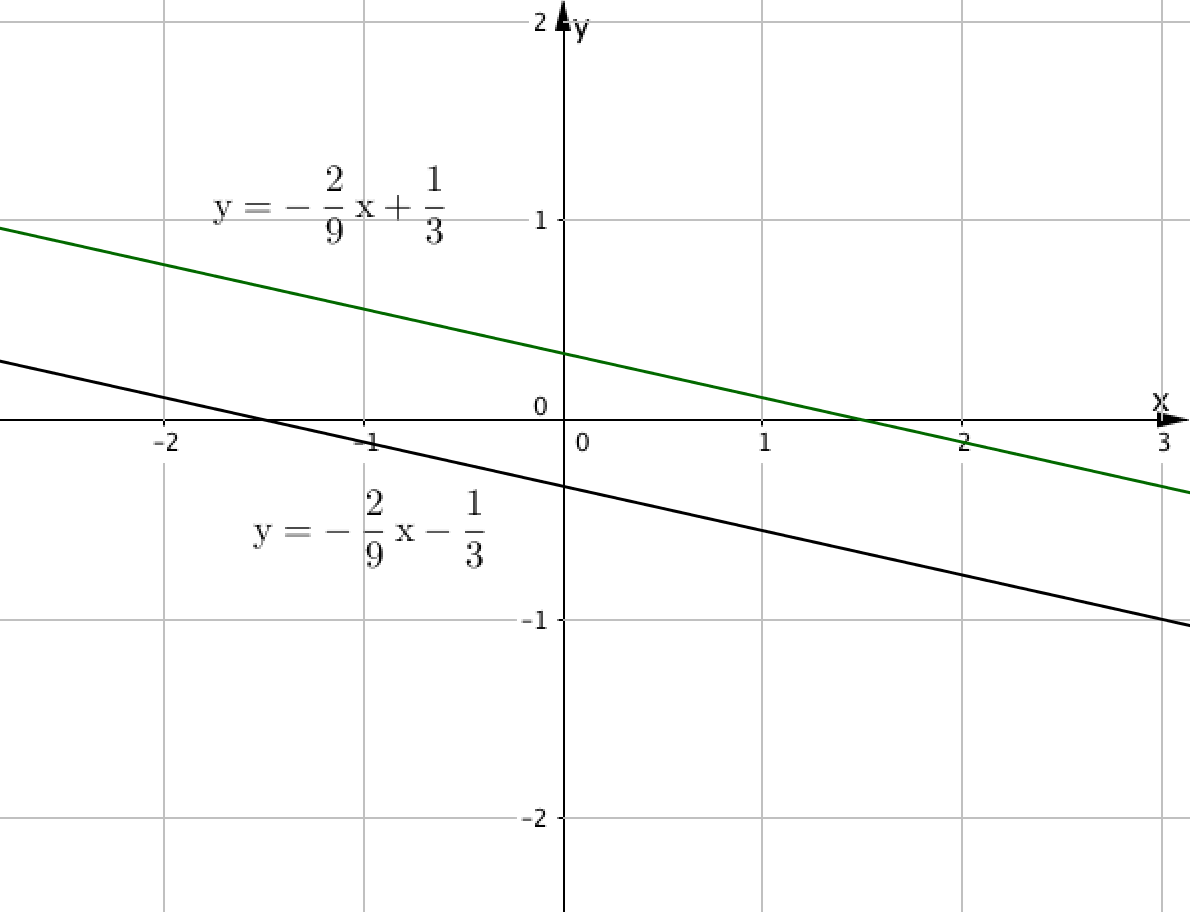
Запишем данные нам уравнения друг над другом:
| \(\displaystyle y=\color{blue}{ -\frac{2}{9}x}-\color{green}{ \frac{1}{3}}{\small , }\) |
| \(\displaystyle y=\color{blue}{ -\frac{2}{9}x}+\color{green}{ \frac{1}{3}}{\small . }\) |
Из данной записи видно, что уравнение \(\displaystyle y=\color{blue}{ -\frac{2}{9}x}+\color{green}{ \frac{1}{3}}\) получено из уравнения \(\displaystyle y=\color{blue}{ -\frac{2}{9}x}-\color{green}{ \frac{1}{3}}\) добавлением \(\displaystyle \color{green}{ \frac{1}{3}}-\left(-\color{green}{ \frac{1}{3}}\right)=\color{green}{ \frac{2}{3}}{\small . } \)
Если поднять график функции \(\displaystyle y=f(x) \) на \(\displaystyle \color{blue}{\rm A} \) единиц вверх, получится график функции \(\displaystyle y=f(x)+\color{blue}{\rm A}{\small . } \)
Согласно правилу, это означает, что прямая \(\displaystyle y=-\frac{2}{9}x+\frac{1}{3}\) получена из прямой \(\displaystyle y=-\frac{2}{9}x-\frac{1}{3}\) сдвигом на \(\displaystyle \bf \frac{2}{3}\) единиц вверх.