Запишите уравнение прямой, полученной с помощью сдвига прямой \(\displaystyle y=-\frac{x}{6}+\frac{1}{2}\) на \(\displaystyle 3\frac{1}{3}\) единицы вниз (вдоль оси \(\displaystyle \rm OY\)).
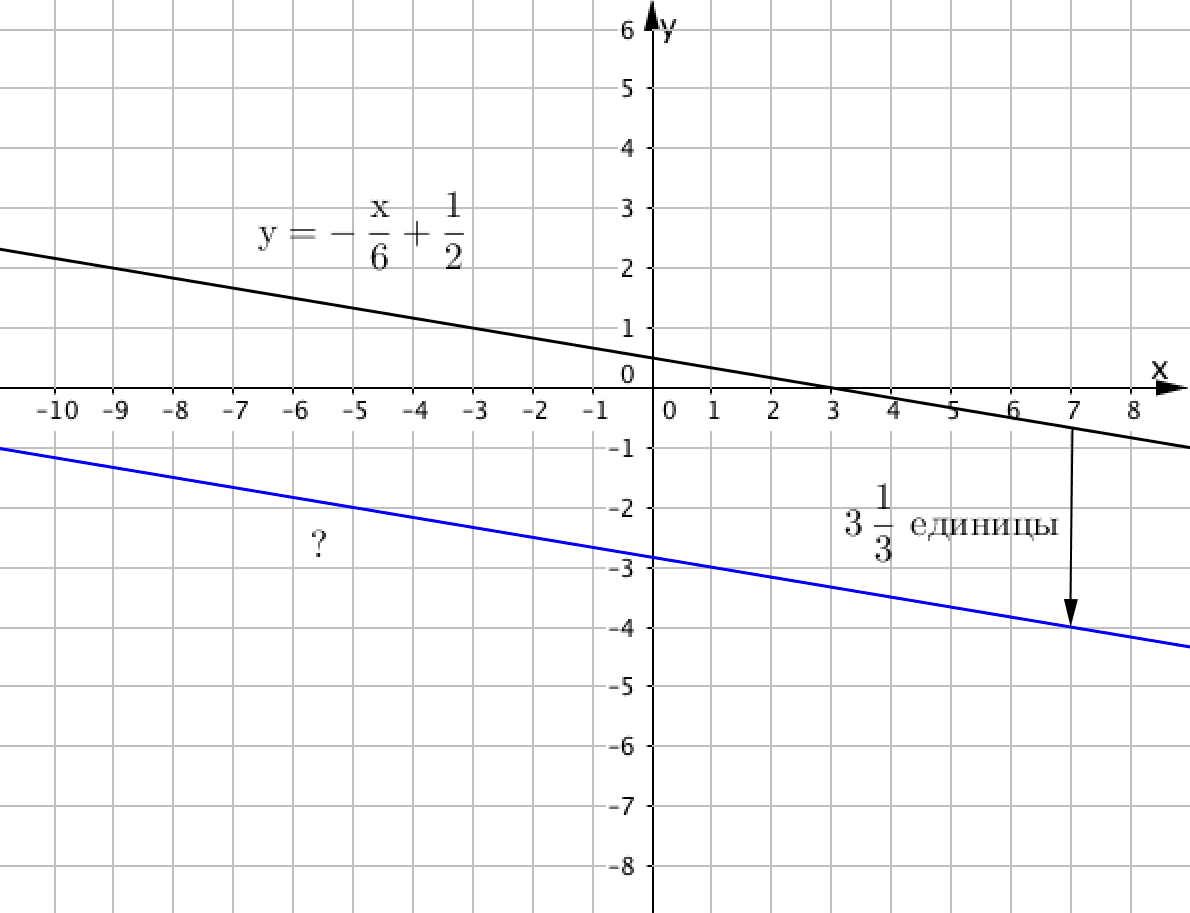
Если опустить график функции \(\displaystyle y=f(x) \) на \(\displaystyle \color{blue}{\rm A} \) единиц вниз, получится график функции \(\displaystyle y=f(x)-\color{blue}{\rm A}{\small . } \)
Нам дан график функции \(\displaystyle y=\color{green}{ -\frac{x}{6}+\frac{1}{2}}{\small , } \) и мы его опускаем на \(\displaystyle \color{blue}{ 3\frac{1}{3}}\) единиц вниз.
Тогда, согласно правилу, у нас получится график функции:
\(\displaystyle y=\left(\color{green}{ -\frac{x}{6}+\frac{1}{2}}\right)-\color{blue}{ 3\frac{1}{3}}=-\frac{x}{6}+\frac{1}{2}-\frac{10}{3}=-\frac{x}{6}-\frac{17}{6}{\small . } \)