На прямой \(\displaystyle a\) отмечены точки \(\displaystyle C\), \(\displaystyle D\) и \(\displaystyle E\).
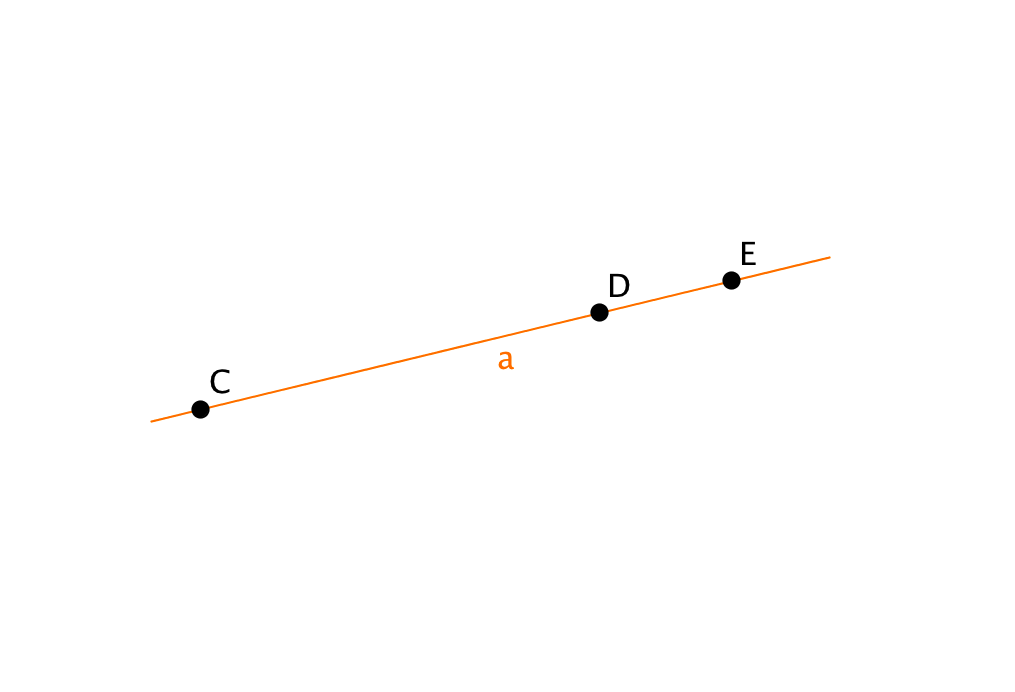
Чему равно количество получившихся при этом лучей и отрезков?
лучей и отрезков(-а)
Часть прямой, ограниченную двумя точками, называют отрезком.
Точка, лежащая на прямой, делит ее на две части. Каждая из этих частей называется лучом с началом в данной точке.
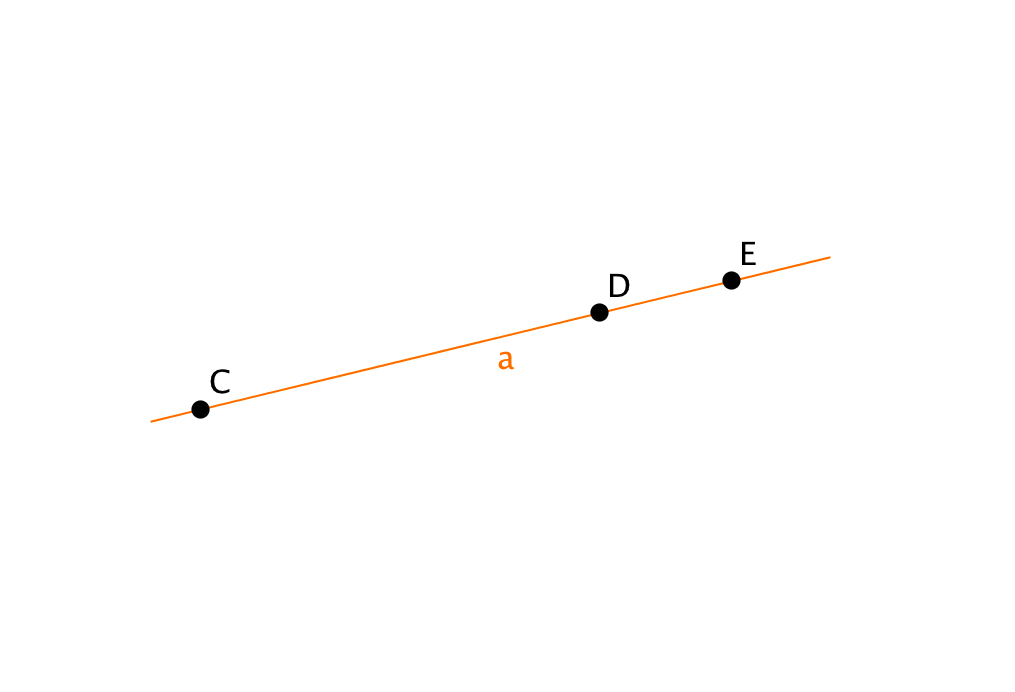
Каждая из трех точек \(\displaystyle C\), \(\displaystyle D\) и \(\displaystyle E\) делит прямую \(\displaystyle a\) на две части, то есть на два луча. Эти точки являются началами каждого из них. Таким образом, получаем всего \(\displaystyle 6\) лучей.
Каждая пара точек \(\displaystyle C\), \(\displaystyle D\) и \(\displaystyle E\) является соответственно началом и концом отрезков: \(\displaystyle CD\), \(\displaystyle DE\) и \(\displaystyle CE\). Таким образом, получаем всего \(\displaystyle 3\) отрезка.
Ответ: \(\displaystyle 6\) лучей и \(\displaystyle 3\) отрезка.