На рисунке изображены три прямые \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), пересекающиеся в точках \(\displaystyle E\), \(\displaystyle I\) и \(\displaystyle J\). Точка \(\displaystyle F\) принадлежит прямой \(\displaystyle b\). Сколько всего отрезков изображено на рисунке?
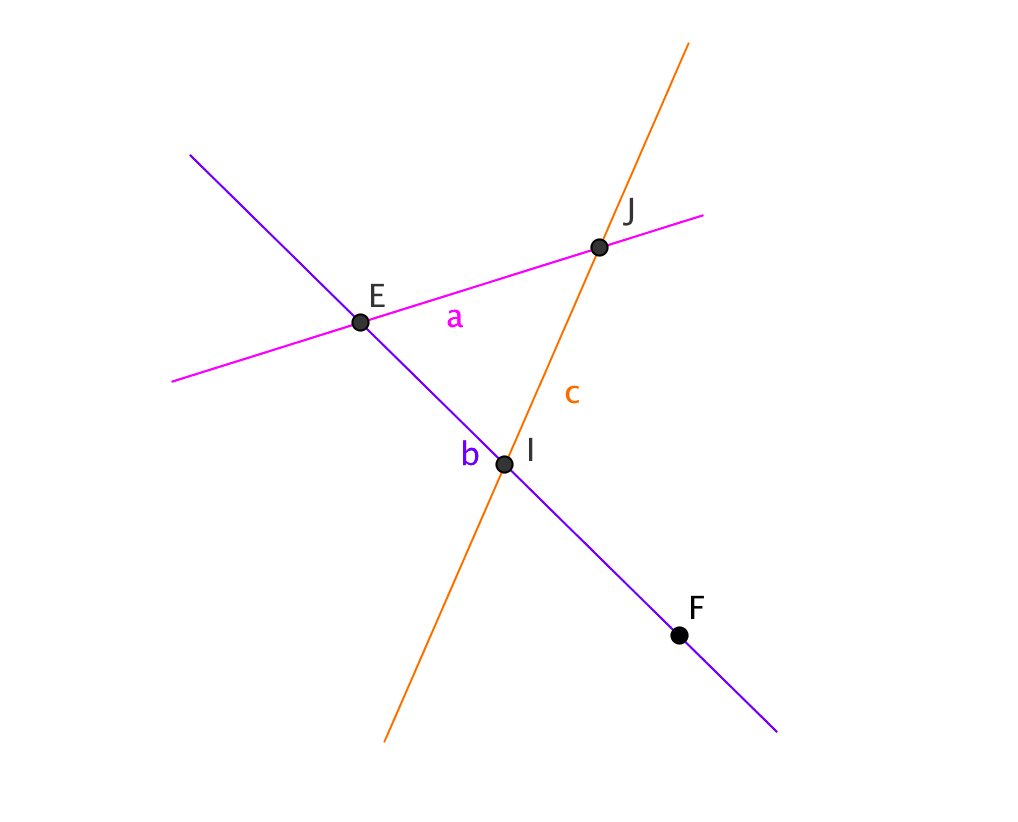
Часть прямой, ограниченную двумя точками, называют отрезком.
На каждой из прямых находятся по две точки ее пересения с другими прямыми. Кроме того, на прямой \(\displaystyle b\) расположена точка \(\displaystyle F\).
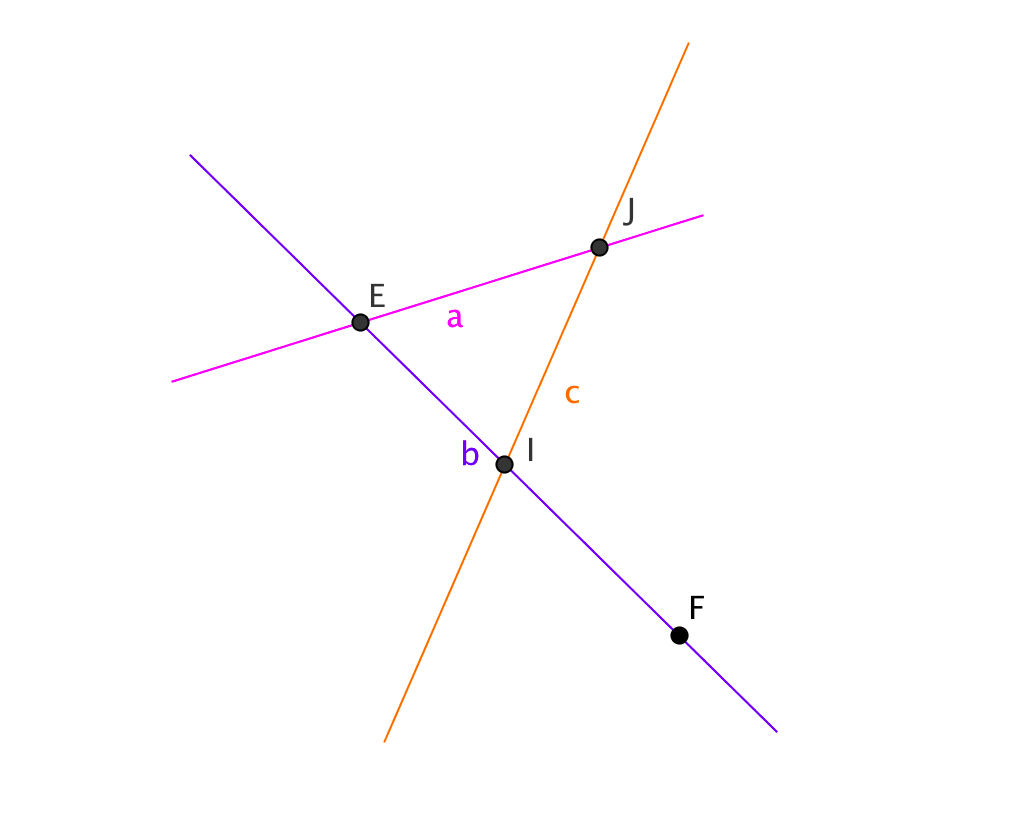
Посчитаем количество отрезков - частей этих прямых, ограниченных данными точками: \(\displaystyle EJ\), \(\displaystyle EI\), \(\displaystyle IJ\), \(\displaystyle EF\), \(\displaystyle IF\). Итого, \(\displaystyle 5\) отрезков.
Ответ: \(\displaystyle 5\) отрезков.