Найдите площадь треугольника, если его основание равно \(\displaystyle 9\) мм, а высота - \(\displaystyle 5\) мм.
, мм2
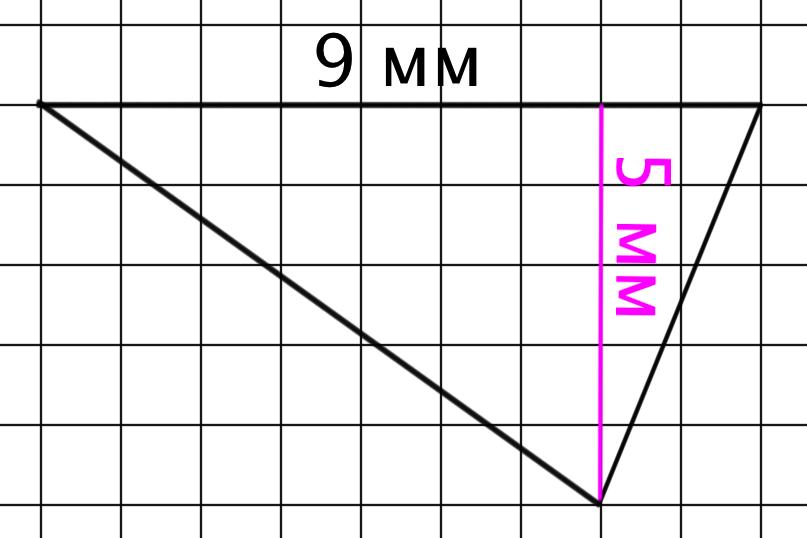
Площадь данного треугольника равна сумме площадей зеленого и серого треугольников.
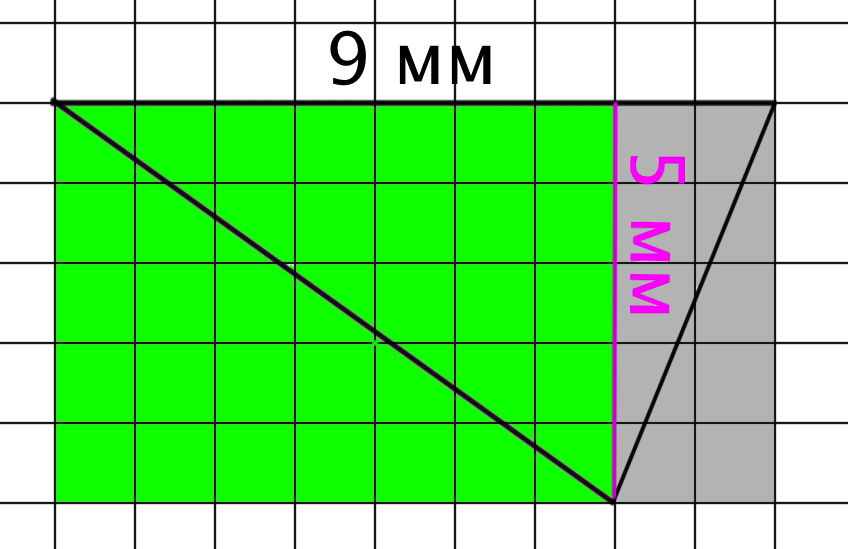
Площадь зеленого треугольника равна половине площади зеленого прямоугольника, а площадь серого треугольника равна половине площади серого прямоугольника.
Значит, площадь данного треугольника равна половине площади прямоугольника, составленного из зеленого и серого прямоугольников. Зеленый и серый прямоугольники образуют один прямоугольник со сторонами \(\displaystyle 9\) мм и \(\displaystyle 5\) мм.
Таким образом, площадь данного треугольника равна половине площади прямоугольника со сторонами \(\displaystyle 9\) мм и \(\displaystyle 5\) мм:
\(\displaystyle \frac{9\cdot 5}{2}=22,5\) мм2.
Ответ: \(\displaystyle 22,5\) мм2.
Мы пришли к выводу, что площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию.