Егер әрбір қиылыста жол кездейсоқ таңдалса (яғни әрбір қиылыста таңдау тең болса) және қозғалыс тек көрсеткі бағытында жүретін болса, \(\displaystyle A\) нүктесінен \(\displaystyle G\) нүктесіне жету ықтималдығын табыңыз.
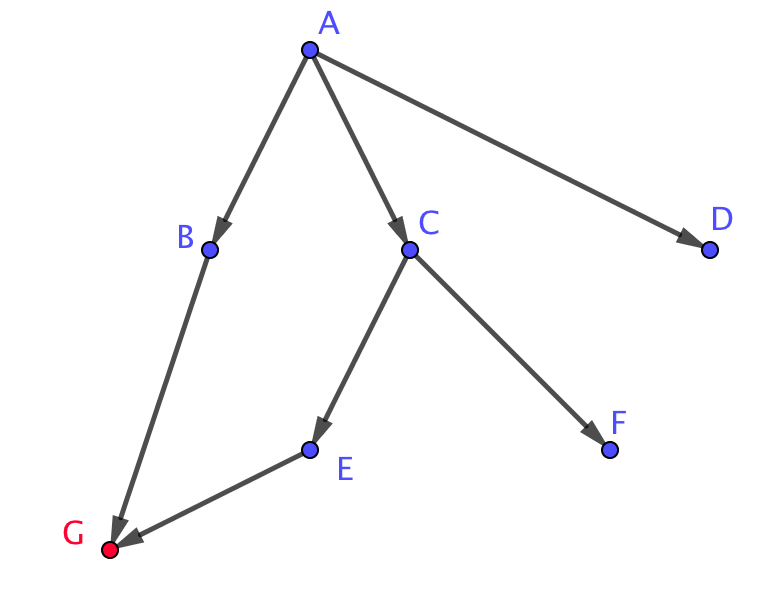
\(\displaystyle А\) нүктесінен \(\displaystyle G\) нүктесіне екі жолмен жетуге болады:
| \(\displaystyle A \rightarrow B \rightarrow G\) | \(\displaystyle A \rightarrow С \rightarrow Е \rightarrow G\) |
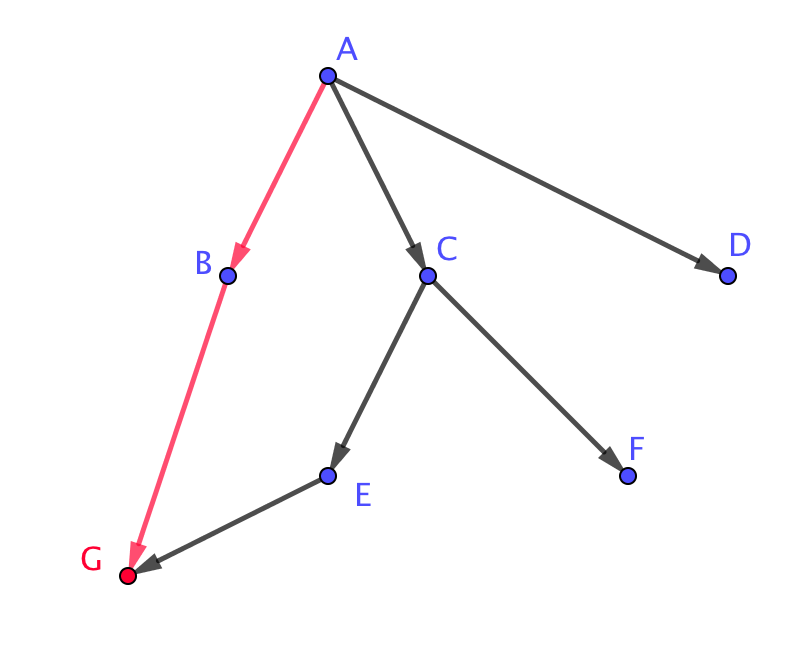 | 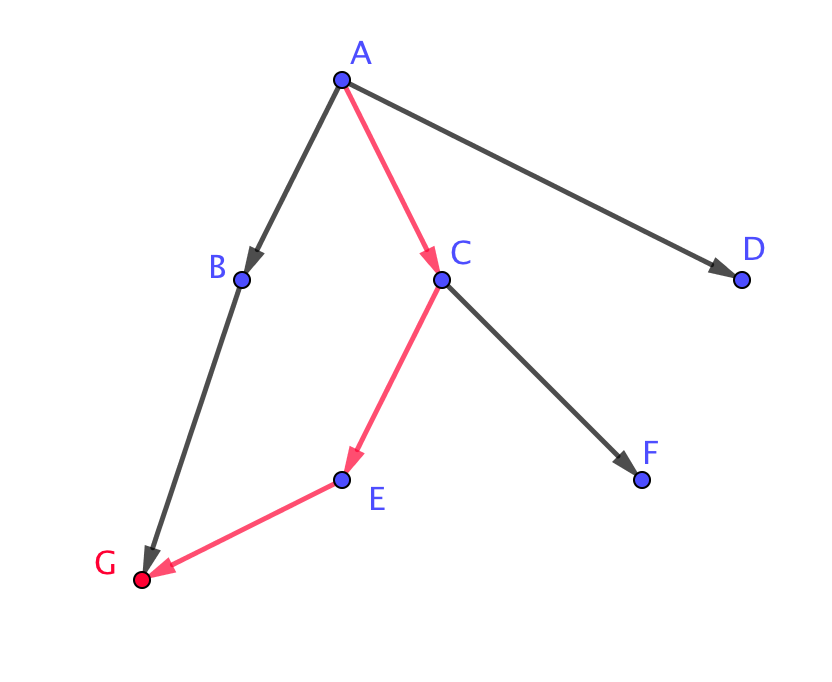 |
Бұл оқиғалар сәйкес келмейтіндіктен (бірден екі жолмен жүруге келмейді), онда
\(\displaystyle P(AG)=P(ABG)+P(ACEG)\) болады.
Осы бағыттардың әрқайсысының жүріп өту ықтималдығын табамыз:
- \(\displaystyle A\) нүктесінен \(\displaystyle B\) нүктесіне жету ықтималдығы \(\displaystyle \frac{1}{3}\) тең, өйткені \(\displaystyle A\) нүктесінен үш жол шығады.
- \(\displaystyle B\) нүктесінен \(\displaystyle G\) нүктесіне жету ықтималдығы \(\displaystyle 1\) тең, өйткені \(\displaystyle B\) нүктесінен бір ғана жол бар.
Сондықтан \(\displaystyle P(ABG)=\frac{1}{3}\cdot 1=\frac{1}{3}{\small .}\)
- \(\displaystyle A\) нүктесінен \(\displaystyle C\) нүктесіне жету ықтималдығы \(\displaystyle \frac{1}{3}\) тең, өйткені \(\displaystyle A\) нүктесінен үш жол шығады.
- \(\displaystyle C\) нүктесінен \(\displaystyle E\) нүктесіне жету ықтималдығы \(\displaystyle \frac{1}{2}\) тең, өйткені \(\displaystyle C\) нүктесінен екі жол шығады.
- \(\displaystyle C\) нүктесінен \(\displaystyle G\) нүктесіне жету ықтималдығы \(\displaystyle 1\) тең, өйткені \(\displaystyle C\) нүктесінен бір ғана жол бар.
Сондықтан \(\displaystyle P(ACEG)=\frac{1}{3}\cdot \frac{1}{2}\cdot 1=\frac{1}{6}{\small .}\)
Осылайша, \(\displaystyle A\) нүктесінен \(\displaystyle G\) нүктесіне жету ықтималдығы
\(\displaystyle P(AG)=P(ABG)+P(ACEG)=\frac{1}{3}+\frac{1}{6}=\frac{3}{6}=0{,}5{\small .}\)
Жауабы:\(\displaystyle 0{,}5{\small .}\)