Нүктенің \(\displaystyle \rm A\) жиынына ену ықтималдығы \(\displaystyle 0{,}7{\small , }\) нүктенің \(\displaystyle \rm B\) жиынына ену ықтималдығы \(\displaystyle 0{,}8{ \small ,}\) және нүктенің \(\displaystyle A \cap B\) түсу ықтималдығы \(\displaystyle 0{,}56{\small . }\) Нүктенің \(\displaystyle \rm A\)немесе \(\displaystyle \rm B{\small }\) жиынына түсу ықтималдығын табыңыз.
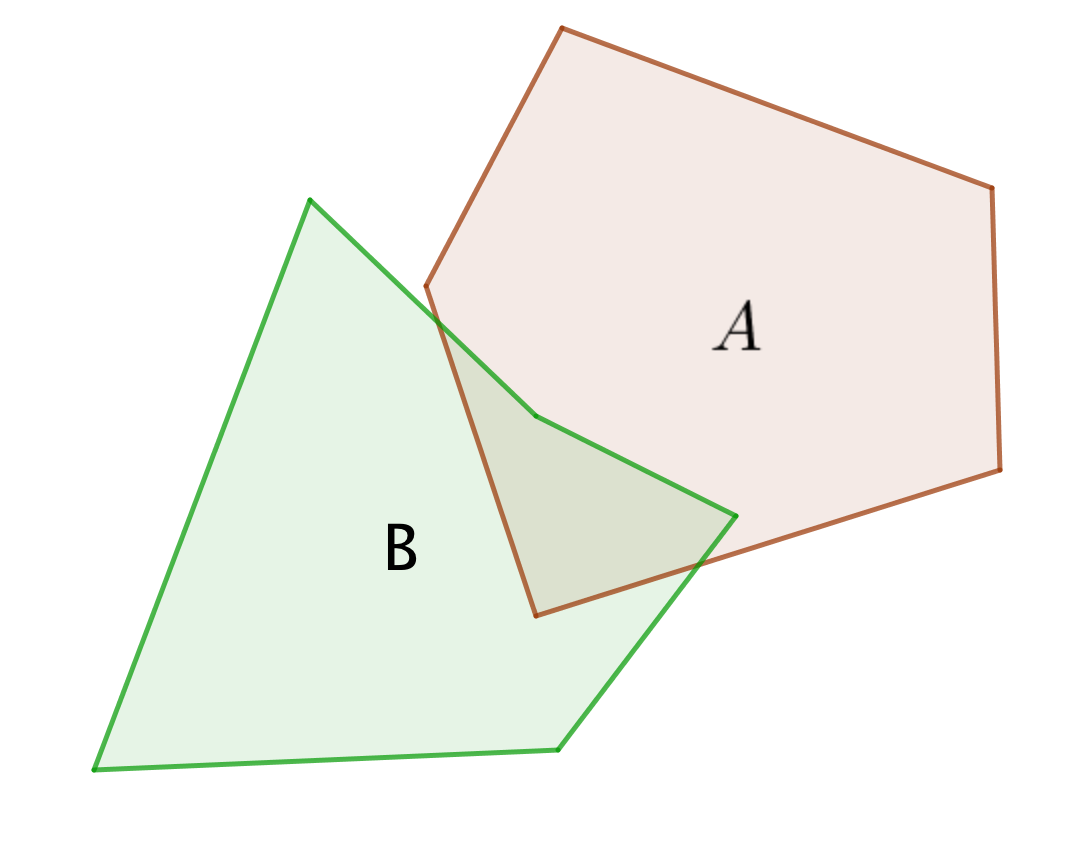
Нүктенің \(\displaystyle \rm A\) жиынына ену ықтималдығы \(\displaystyle 0{,}7{\small , }\) нүктенің \(\displaystyle \rm B\) жиынына ену ықтималдығы \(\displaystyle 0{,}8{\small . }\) Сондай-ақ, бұл оқиғалар тәуелсіз екені белгілі.

\(\displaystyle A \cup B\) фигурасының ауданы \(\displaystyle A\) және \(\displaystyle B\) фигураларының аудандарының қосындысына және одан \(\displaystyle A\cap B\) алынады, өйткені қиылысу екі жиынға да енеді және қосқанда екі рет есептелетіндіктен
\(\displaystyle P(A \cup B)=P(A)+P(B)-P(A\cap B)\)
немесе
\(\displaystyle P(A + B)=P(A)+P(B)-P(A\cdot B){\small .}\)
Осылайша,
\(\displaystyle P(A + B)=0{,}7+0{,}8-0{,}56=0{,}94{\small .}\)
Жауабы:\(\displaystyle 0{,}94{\small .}\)