\(\displaystyle y=k(x-a)^2+b\) функциясының \(\displaystyle k,\,a\) және \(\displaystyle b\) параметрлерін өзгерту арқылы (жүздікке дейін дәл),
\(\displaystyle y=3x^2-12x+13{\small }\) функцияның графигін салыңыз
Нүктелердің координаттарын жазу
\(\displaystyle \color{green}{S}=(\)\(\displaystyle ;\)\(\displaystyle )\)
ондыққа дейін
Параболаның төбесінің координаттары
Егер парабола \(\displaystyle y=ax^2+bx+c{\small }\) теңдеуімен берілсе, онда төбенің координаталарын мына формулалар арқылы табуға болады:
\(\displaystyle x_{0}=\frac{-b}{2a}\)
және
теңдеуде \(\displaystyle x_0\) орнына қойып \(\displaystyle y_0{\small }\) табуға болады.
Теңдеу үшін
\(\displaystyle y=3x^2-12x+13{\small .}\)
\(\displaystyle a=3,\, b=-12\) және \(\displaystyle c=13{\small .}\)
Содан кейін
\(\displaystyle x_0=-\frac{-12}{2\cdot 3},\) яғни \(\displaystyle x_0=2{\small .}\)
\(\displaystyle x_0=2\)-ні \(\displaystyle y=3x^2-12x+13{\small }\) теңдеуіне ауыстырсақ, аламыз.
\(\displaystyle y_0=3\cdot 2^2-12\cdot 2+13{\small ,}\)
\(\displaystyle y_0=1{\small .}\)
Осылайша, шыңның координаталары \(\displaystyle (2;\,1){\small } \) болады.
Еске салайық
\(\displaystyle y=k(x-a)^2+b\) теңдеуімен берілген параболаның төбесі
\(\displaystyle y=k(x-a)^2+b{ \small ,}\)теңдеуімен берілген параболаның төбесі \(\displaystyle (a;\,b){\small}\) координаталары бар нүкте.
Біз \(\displaystyle (2;1){\small }\) шыңды таптық:
Сонда бұл график кейбір \(\displaystyle \color{red}{k}{\small }\)коэффициент үшін \(\displaystyle y=\color{red}{k}(x-2)^2+1\) теңдеуімен беріледі.
Шарт бойынша \(\displaystyle y=\color{red}{3}x^2-12x+13{\small }\) функцияның графигі берілген
Демек, \(\displaystyle \color{red}{k}=\color{red}{3}\) және берілген параболаны теңдеу арқылы беруге болады
\(\displaystyle y=3(x-2)^2+1{\small .}\)
\(\displaystyle y=k x^2{ \small ,}\) мәнінен \(\displaystyle y=3(x-2)^2+1\) алу үшін сізге қажет:
- \(\displaystyle k=3{ \small } \) мәнің орнатамыз,
- графикті \(\displaystyle \rm OX{\small }\) ось бойымен екі бірлік оңға жылжытыңыз
- диаграмманы \(\displaystyle \rm OY{\small }\) ось бойымен бір бірлікке жоғары жылжытыңыз
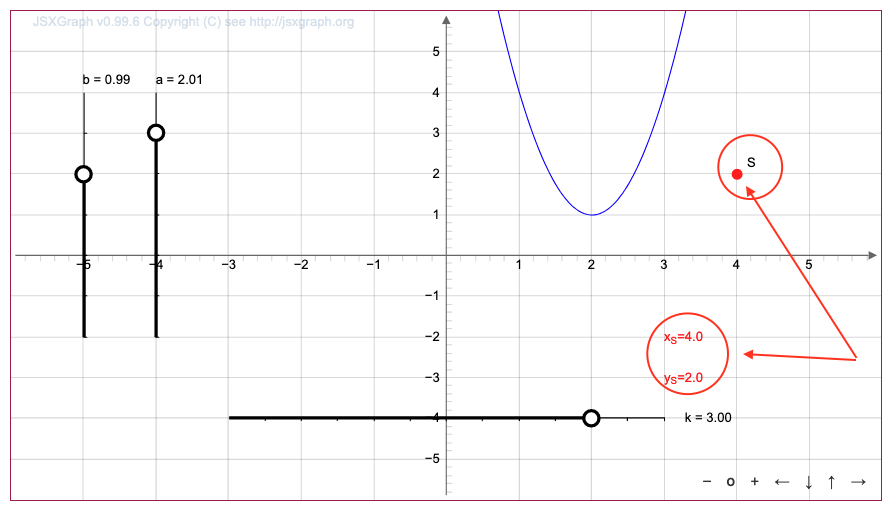
Сонда \(\displaystyle S \) нүктесінің координаттары \(\displaystyle (4;\,2){\small } \) болады