Формуланы геометриялық тәсілмен дәлелдейік:
Кез келген оң \(\displaystyle a,\, b\) сандары үшін келесі тепе-теңдік дұрыс:
\(\displaystyle (a+b\,)(a-b\,)=a^{\,2}-b^{\, 2}.\)
Айқындық үшін біз \(\displaystyle a>b\) деп санаймыз.
\(\displaystyle (a-b\,)(a+b\,)\) көбейтіндісі қабырғалары \(\displaystyle (a-b\,)\) және \(\displaystyle (a+b\,)\) болатын тіктөртбұрыштың ауданы болып табылады. Аталған тіктөртбұрыш салайық:
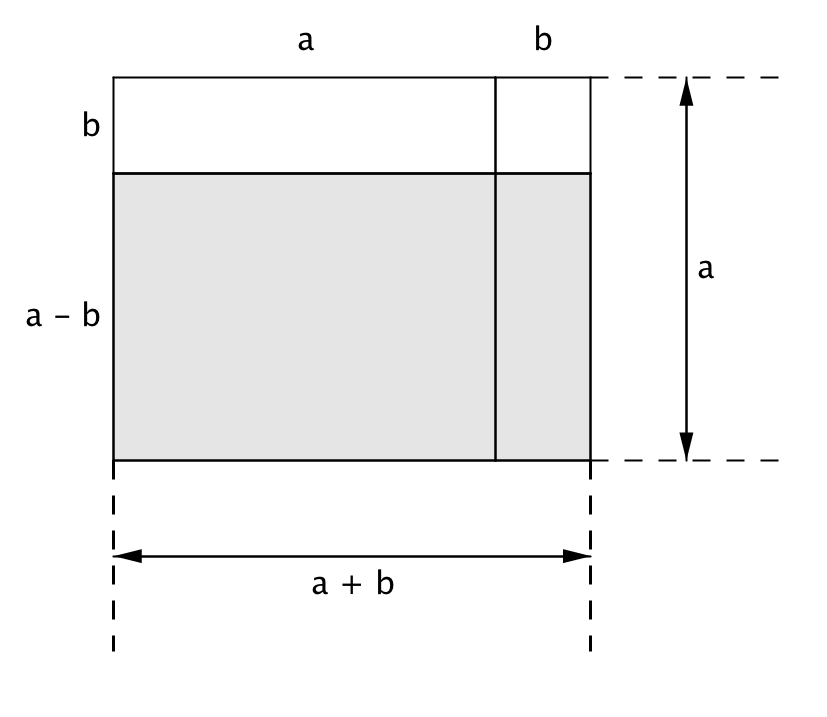
Бұл тіктөртбұрыштың ауданы (сұр түске боялған) оның қабырғаларының ұзындығының, яғни \(\displaystyle (a-b\,)(a+b\,)\) көбейтіндісіне тең:
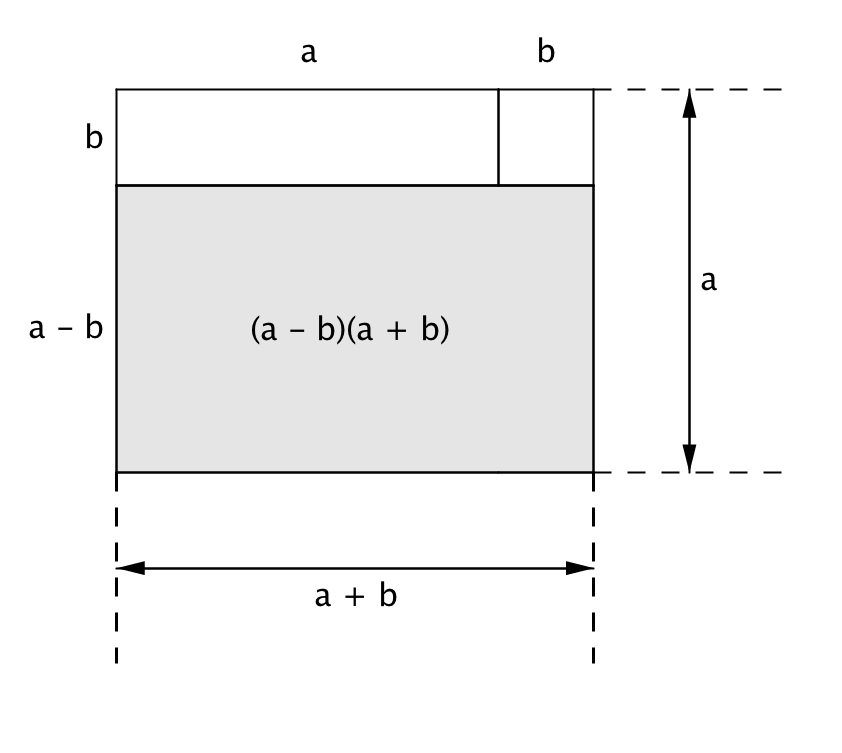
Осы тіктөртбұрыштың ауданын басқа әдіспен есептейік.
Бұл аудан екі тіктөртбұрыштың аудандарының қосындысына тең: \(\displaystyle (a-b\,)\) және қабырғалары \(\displaystyle a\) болатын "1" тіктөртбұрыштың ауданы
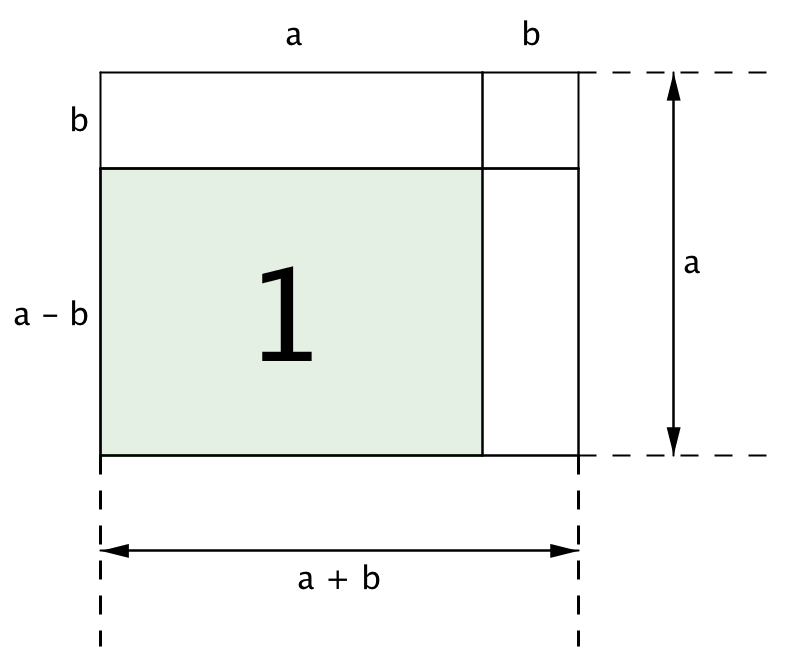
және қабырғалары \(\displaystyle (a-b\,)\) және \(\displaystyle b\) болатын "2" тіктөртбұрышының аудандары
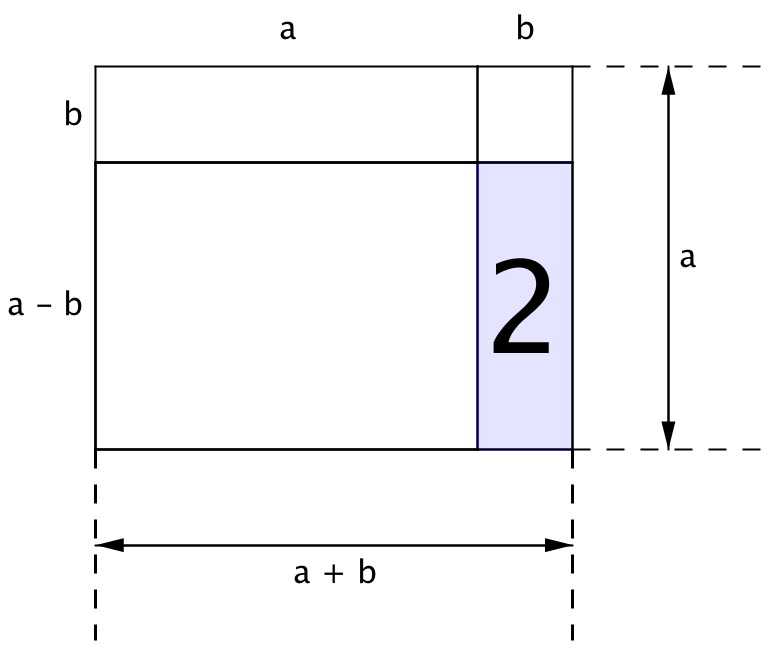
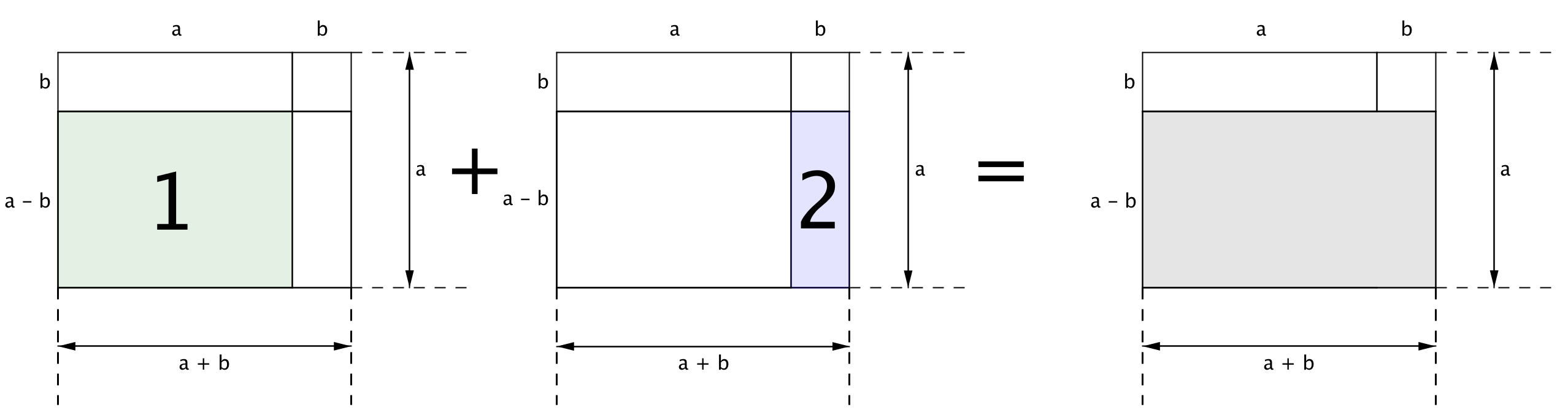
Тіктөртбұрыштардың әрқайсысының ауданын тауып, оларды қосайық. Нәтижесінде осы тіктөртбұрыштың ауданын аламыз.
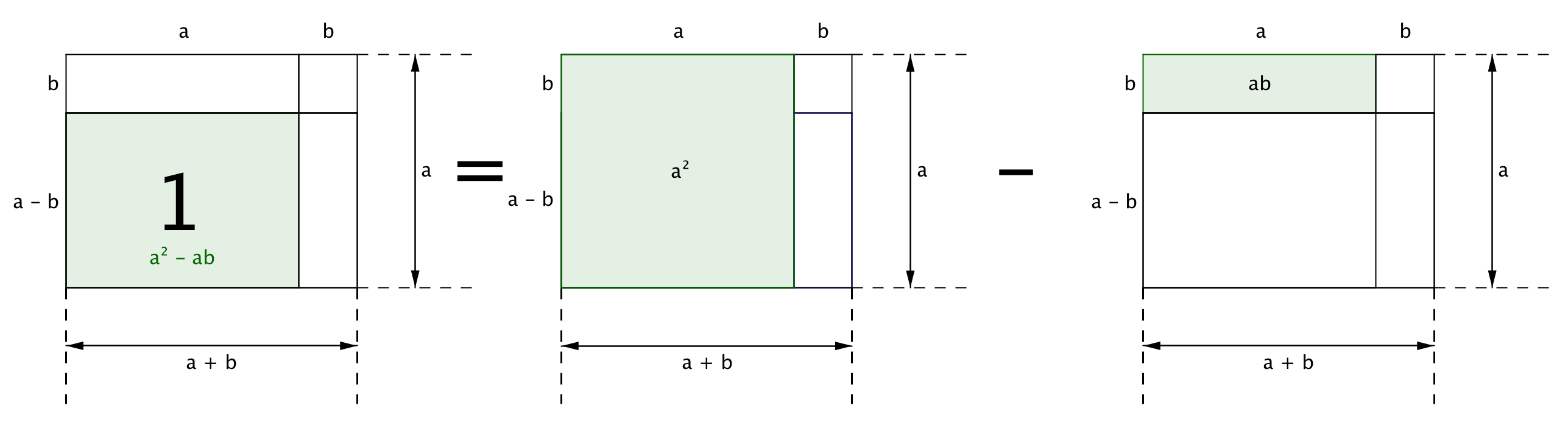
"1" тіктөртбұрышының ауданы қабырғасы \(\displaystyle a\) болатын шаршының және қабырғалары \(\displaystyle a\) және \(\displaystyle b\) болатын тіктөртбұрыштың аудандарының айырмасына тең:
\(\displaystyle a^{\,2}-ab\)
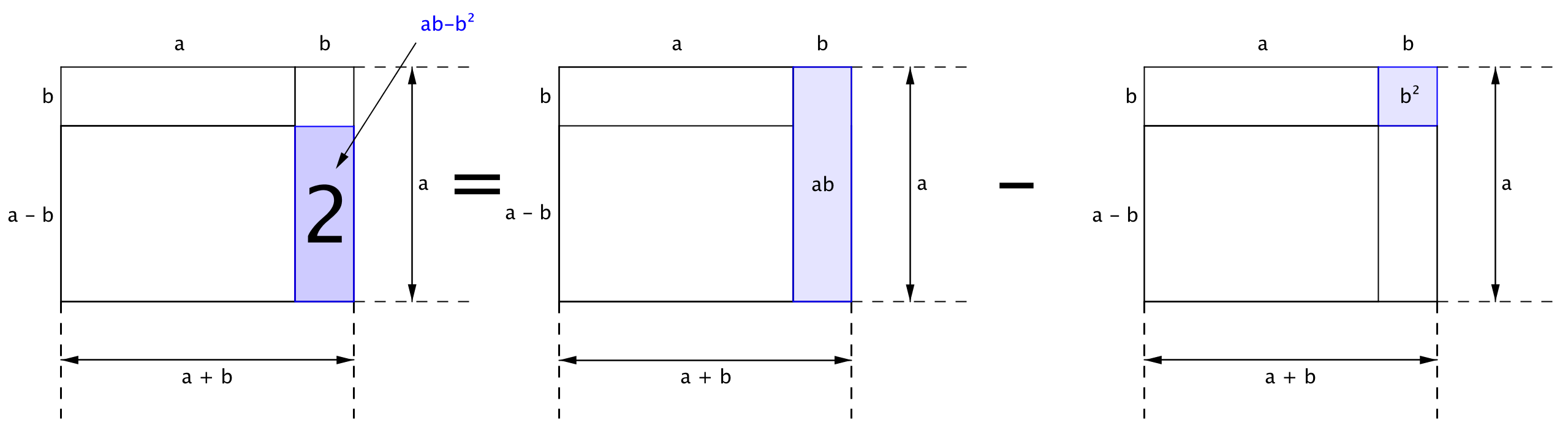
"2" тіктөртбұрышының ауданы қабырғалары \(\displaystyle a\) және \(\displaystyle b\) болатын тіктөртбұрыштың және қабырғасы \(\displaystyle b\) болатын шаршының аудандарының айырмасына тең:
\(\displaystyle ab-b^{\,2}\)
Осылайша, қабырғалары \(\displaystyle (a-b\,)\) және \(\displaystyle (a+b\,)\) болатын тіктөртбұрыштың ауданы "1" және "2" тіктөртбұрыштардың аудандарының қосындысына тең:
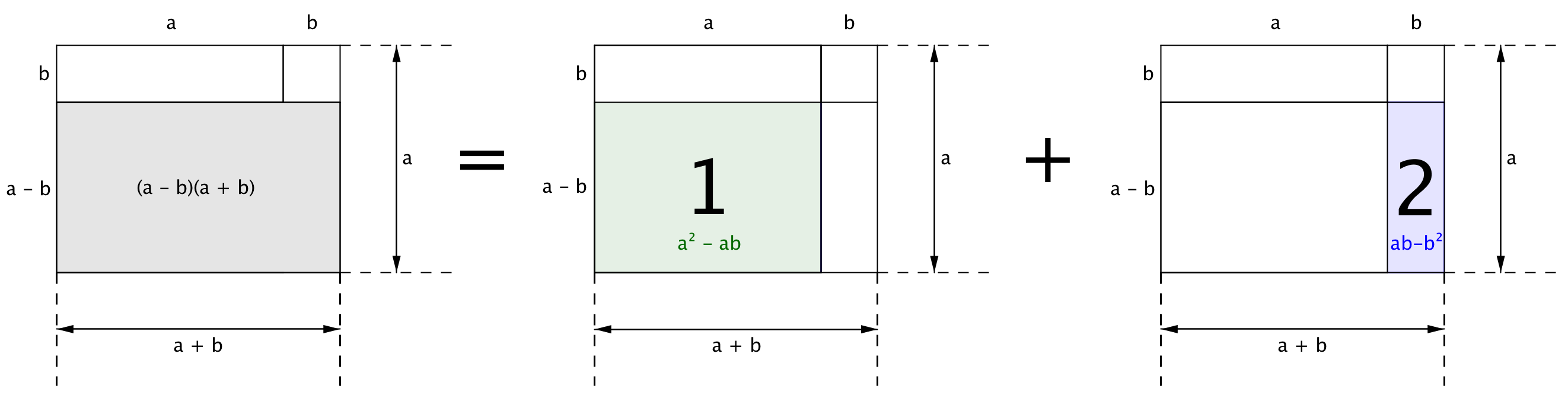
\(\displaystyle (a-b\,)(a+b\,)=(a^2-ab\,)+(ab-b^2\,).\)
Жақшаларды ашайық:
\(\displaystyle (a-b\,)(a+b\,)=(a^{\,2}-ab\,)+(ab-b^{\,2}\,)=a^{\,2}-ab+ab-b^{\,2}=a^{\,2}-b^{\,2}.\)
Осылайша, біз "квадраттар айырмасы" формуласын геометриялық тәсілмен дәлелдедік.