Сызықтық теңдеулер жүйесі берілген
\(\displaystyle \left\{\begin{aligned}3x-2y+5=&6-x{\small , }\\2x+3y-1=&1{,}5+4y\end{aligned}\right.\)
және екі сызықтық функцияның графиктері:
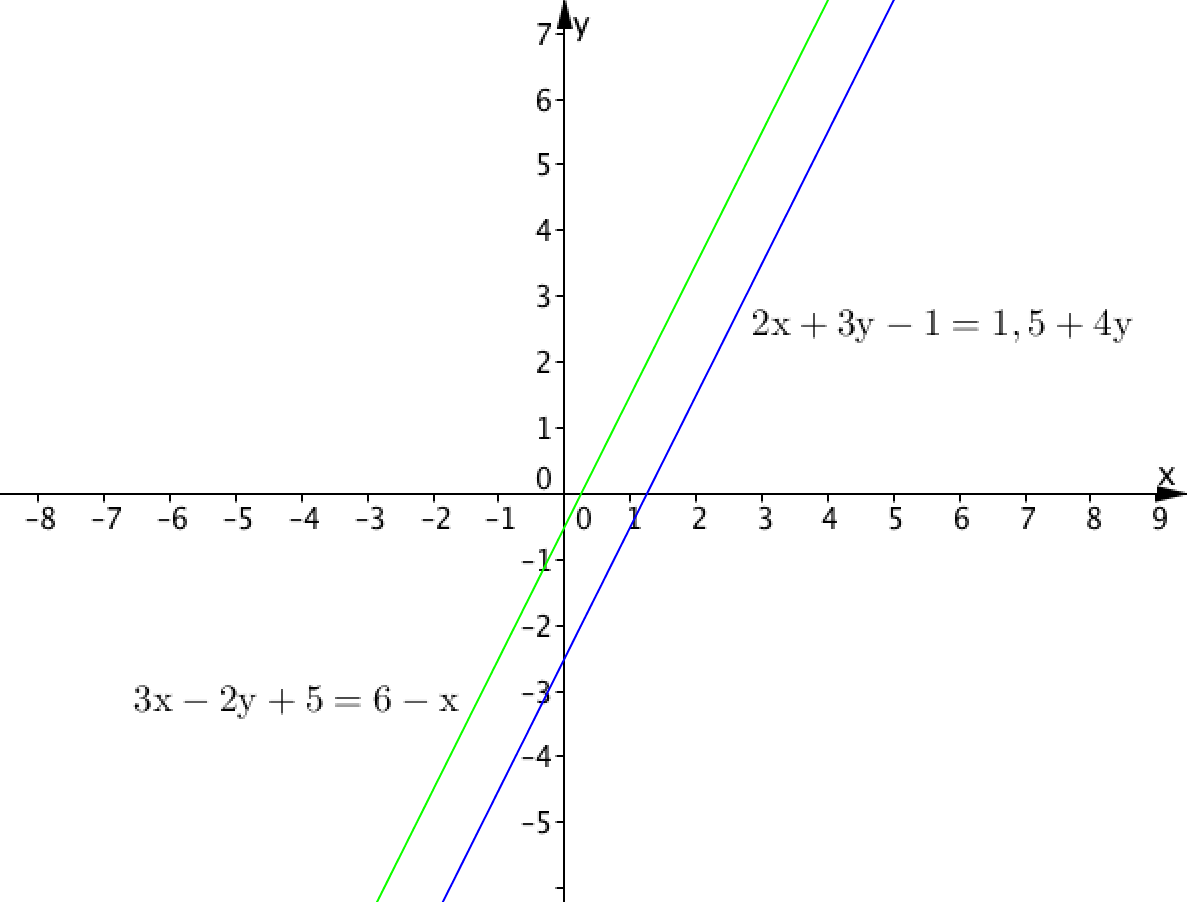
Сызықтық теңдеулер жүйесінің шешімдерінің санын анықтаңыз
Бізге сызықтық теңдеулер жүйесі берілген
\(\displaystyle \left\{\begin{aligned}3x-2y+5=&6-x{\small , }\\2x+3y-1=&1{,}5+4y{\small . }\end{aligned}\right.\)
Координаталық жазықтықтағы әрбір сызықтық теңдеу түзуге сәйкес келетінін білеміз.
Үш жағдай болуы мүмкін:
1) теңдеулерге сәйкес келетін түзулер бір нүктеде қиылысады, содан кейін жүйенің жалғыз шешімі болады;
2) теңдеулерге сәйкес келетін сызықтар қиылыспайды (параллель), содан кейін жүйенің шешімдері болмайды;
3) теңдеулерге сәйкес келетін түзулер сәйкес келеді, содан кейін жүйеде шексіз көптеген шешімдер бар.
Суретте бізге берілген жүйенің теңдеулеріне сәйкес келетін сызықтар көрсетілген. Олар қиылыспайтындықтан (параллель), жүйенің шешімдері жоқ.
Жауап: шешімі жоқ