Сызықтық теңдеулер жүйесі берілген
\(\displaystyle \left\{\begin{aligned}&x+{\small \frac{2y}{3}}+{\small \frac{1}{3}}=1+{\small \frac{x}{3}}{\small , }\\&2x-y=1+x-2y\end{aligned}\right.\)
және екі сызықтық функцияның графиктері:
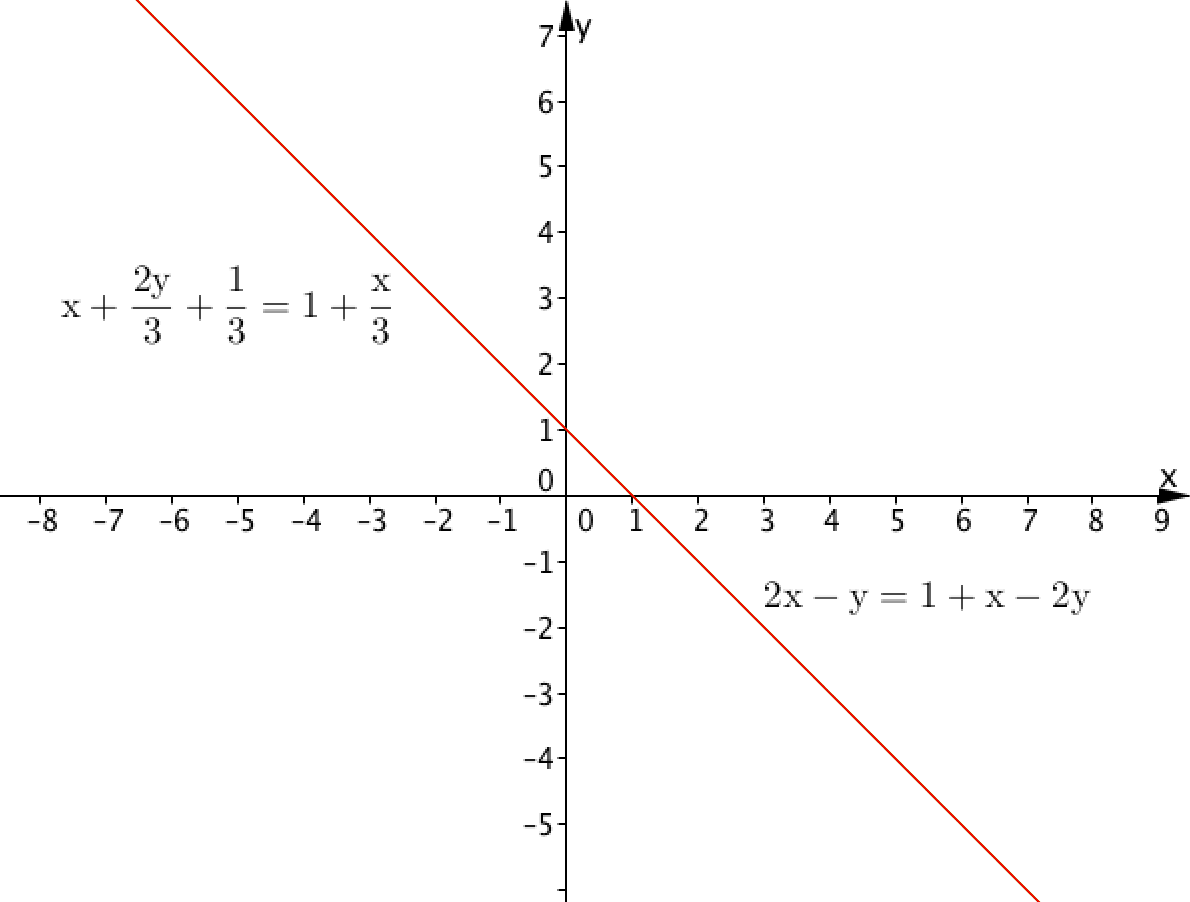
Сызықтық теңдеулер жүйесінің шешімдерінің санын анықтаңыз.
Бізге сызықтық теңдеулер жүйесі берілген
\(\displaystyle \begin{array}{rl}\left\{\vphantom{\begin{aligned}1\\{\small \frac{2}{3}}\end{aligned}}\right.&\kern{-1.5em}\begin{aligned}&x+{\small \frac{2y}{3}}+{\small \frac{1}{3}}=1+{\small \frac{x}{3}}{\small , }\\&2x-y=1+x-2y{\small . }\end{aligned}\end{array}\)
Координаталық жазықтықтағы әрбір сызықтық теңдеу түзуге сәйкес келетінін білеміз.
Үш жағдай болуы мүмкін:
1) теңдеулерге сәйкес келетін түзулер бір нүктеде қиылысады, содан кейін жүйенің жалғыз шешімі болады;
2) теңдеулерге сәйкес келетін сызықтар қиылыспайды (параллель), содан кейін жүйенің шешімдері болмайды;
3) теңдеулерге сәйкес келетін түзулер сәйкес келеді, содан кейін жүйеде шексіз көптеген шешімдер бар.
Суретте бізге берілген жүйенің теңдеулеріне сәйкес келетін сызықтар көрсетілген. Олар сәйкес келетіндіктен, жүйеде шексіз көптеген шешімдер бар.
Жауап: шексіз көптеген шешімдер.