\(\displaystyle y=x^2{\small }\) квадраттық функциясы берілген. Берілген нүктелердегі функция мәндерін есептеңіз:
| \(\displaystyle x\) | \(\displaystyle -2\) | \(\displaystyle -1{,}7\) | \(\displaystyle -1{,}5\) | \(\displaystyle -1\) | \(\displaystyle -0{,}5\) | \(\displaystyle 0\) | \(\displaystyle 0{,}5\) | \(\displaystyle 1\) | \(\displaystyle 1{,}5\) | \(\displaystyle 1{,}7\) | \(\displaystyle 2\) |
| \(\displaystyle y=x^2\) |
Осы \(\displaystyle y=x^2{\small }\) квадраттық функцияда орналасқан нүктелері бар дұрыс графикті таңдаңыз:
| \(\displaystyle \rm I\) | \(\displaystyle \rm II\) |
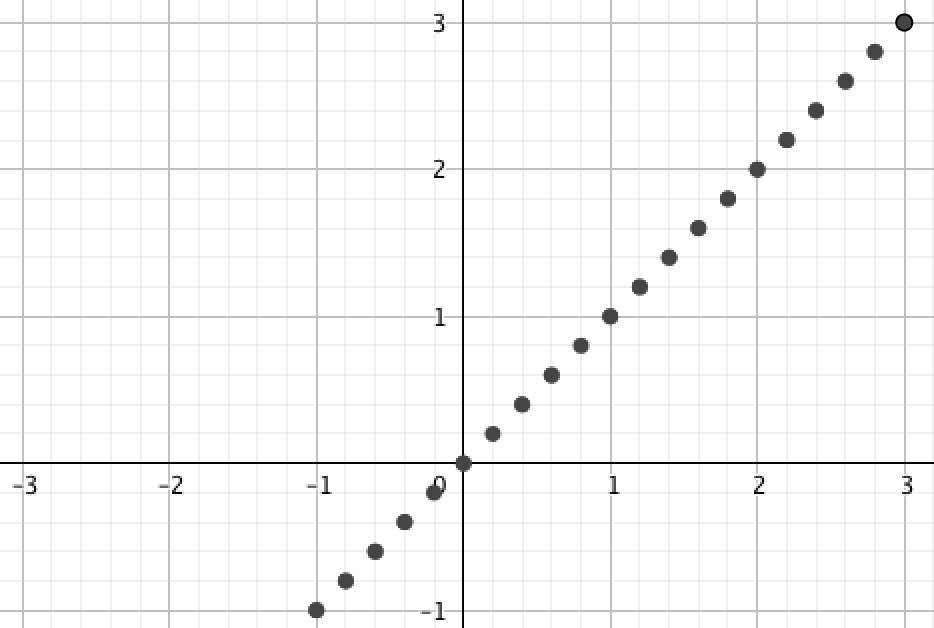 | 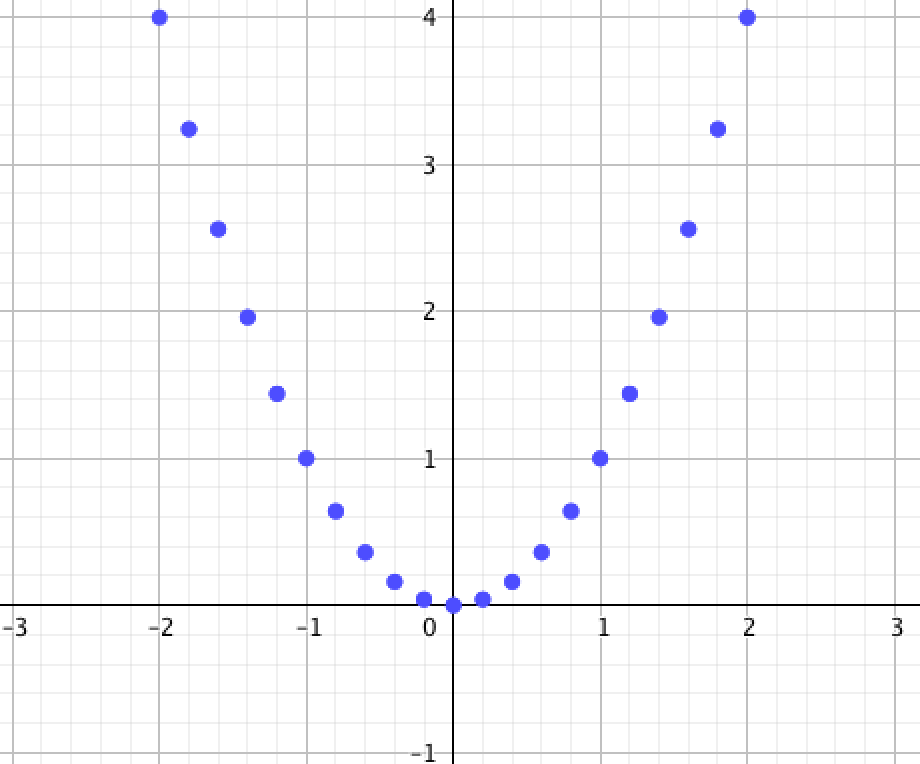 |
| \(\displaystyle \rm III\) | \(\displaystyle \rm IV\) |
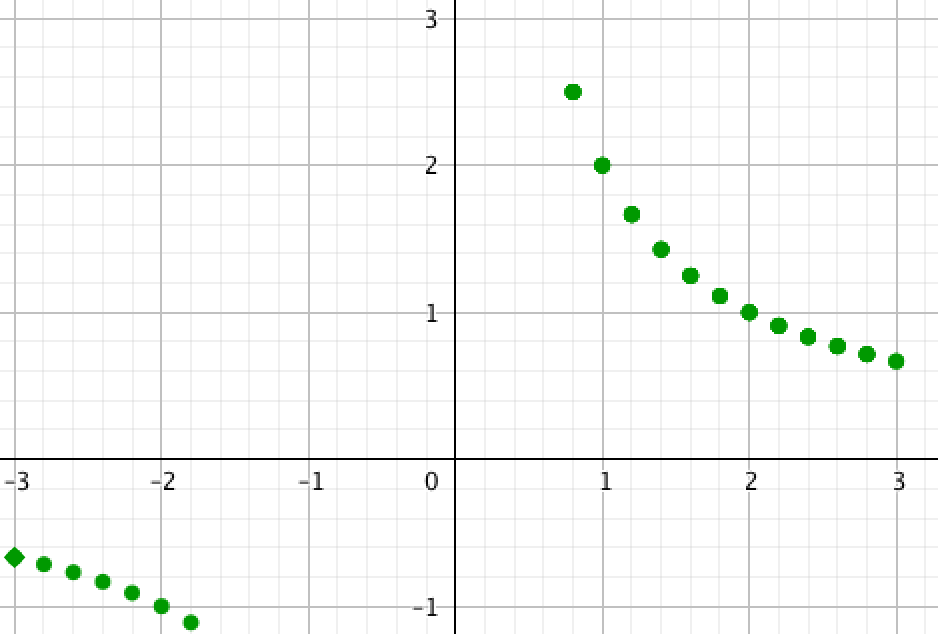 | 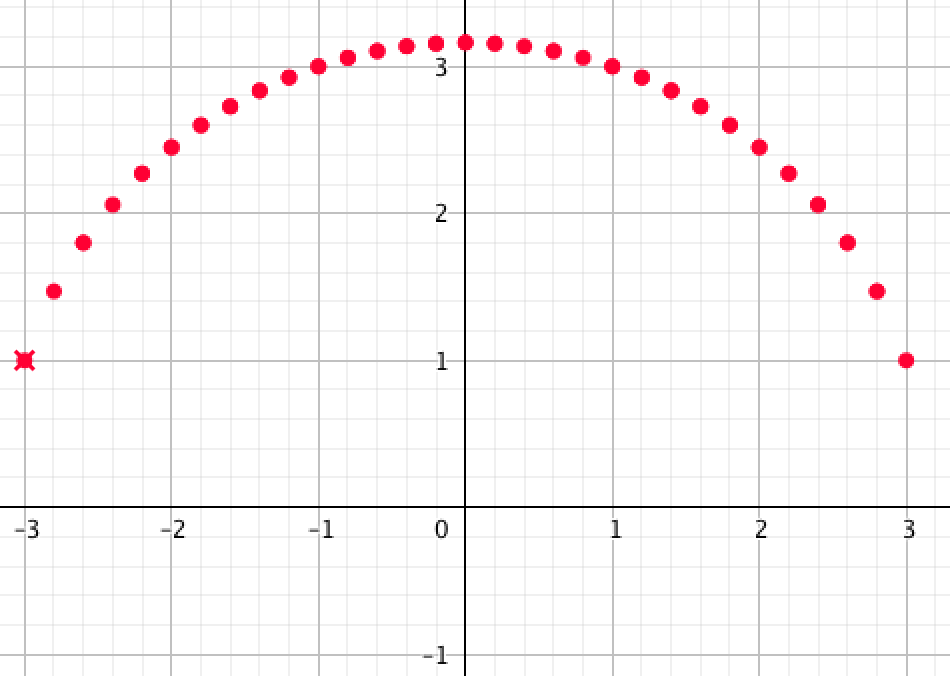 |
Берілген нүктелердегі \(\displaystyle y=x^2\) квадраттық функциясының мәнін есептейік:
| \(\displaystyle x\) | \(\displaystyle -2\) | \(\displaystyle -1{,}7\) | \(\displaystyle -1{,}5\) | \(\displaystyle -1\) | \(\displaystyle -0{,}5\) | \(\displaystyle 0\) | \(\displaystyle 0{,}5\) | \(\displaystyle 1\) | \(\displaystyle 1{,}5\) | \(\displaystyle 1{,}7\) | \(\displaystyle 2\) |
| \(\displaystyle y=x^2\) | \(\displaystyle 4\) | \(\displaystyle 2{,}89\) | \(\displaystyle 2{,}25\) | \(\displaystyle 1\) | \(\displaystyle 0{,}25\) | \(\displaystyle 0\) | \(\displaystyle 0{,}25\) | \(\displaystyle 1\) | \(\displaystyle 2{,}25\) | \(\displaystyle 2{,}89\) | \(\displaystyle 4\) |
Координаталық жазықтықта
\(\displaystyle (-2;\, 4),\, (-1{,}7;\, 2{,}89),\, (-1{,}5;\, 2{,}25),\, (-1;\, 1),\, (-0{,}5;\, 0{,}25),\, (0;\, 0),\)
\(\displaystyle (0{,}5;\, 0{,}25),\, (1;\, 1),\, (1{,}5;\, 2{,}25),\, (1{,}7;\, 2{,}89),\,(2;\, 4)\)
нүктелерін белгілейік:
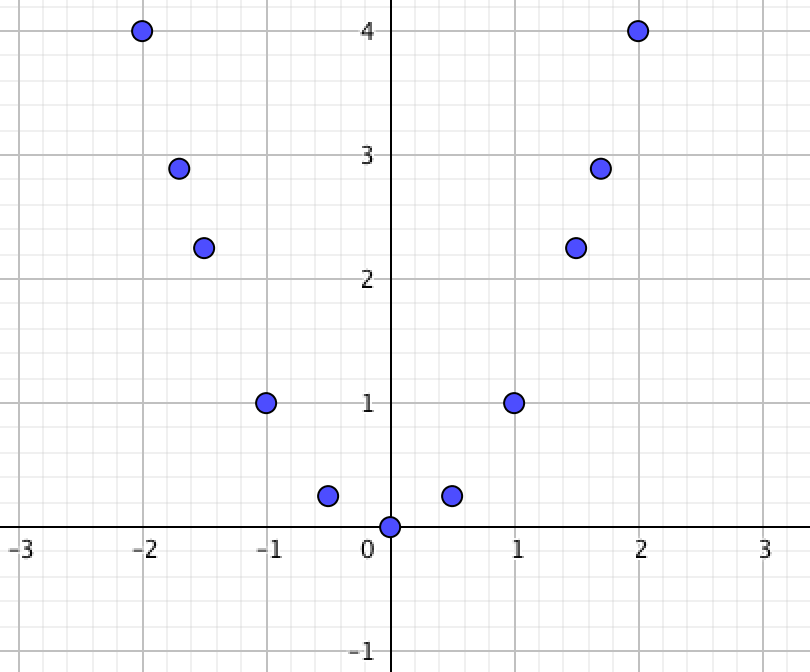
Берілген графиктермен салыстырайық:
| \(\displaystyle \rm I\) | \(\displaystyle \rm II\) |
 |  |
| \(\displaystyle \rm III\) | \(\displaystyle \rm IV\) |
 |  |
\(\displaystyle \rm II\) графигі біздің \(\displaystyle y=x^2{\small }\) квадраттық функциямызға сәйкес келетінін көреміз.
Жауабы: \(\displaystyle \rm II {\small .}\)