Тапсырма
\(\displaystyle [-1; 1] \small \) кесіндісінде \(\displaystyle y=2x^2\) квадраттық функциясының графигін салу.
Шешім
\(\displaystyle y=2x^2{\small }\) квадраттық функциясы мәндерінің кестесін толтырайық:
| \(\displaystyle x\) | \(\displaystyle -1\) | \(\displaystyle -0{,}8\) | \(\displaystyle -0{,}6\) | \(\displaystyle -0{,}4\) | \(\displaystyle -0{,}3\) | \(\displaystyle 0\) | \(\displaystyle 0{,}3\) | \(\displaystyle 0{,}4\) | \(\displaystyle 0{,}6\) | \(\displaystyle 0{,}8\) | \(\displaystyle 1\) |
| \(\displaystyle y=2x^2\) | \(\displaystyle 2\cdot (-1)^2\) | \(\displaystyle 2\cdot (-0{,}8)^2\) | \(\displaystyle 2\cdot (-0{,}6)^2\) | \(\displaystyle 2\cdot (-0{,}4)^2\) | \(\displaystyle 2\cdot (-0{,}3)^2\) | \(\displaystyle 0\) | \(\displaystyle 2\cdot 0{,}3^2\) | \(\displaystyle 2\cdot 0{,}4^2\) | \(\displaystyle 2\cdot 0{,}6^2\) | \(\displaystyle 2\cdot 0{,}8^2\) | \(\displaystyle 2\cdot 1^2\) |
Мәндерді есептейміз:
| \(\displaystyle x\) | \(\displaystyle -1\) | \(\displaystyle -0{,}8\) | \(\displaystyle -0{,}6\) | \(\displaystyle -0{,}4\) | \(\displaystyle -0{,}3\) | \(\displaystyle 0\) | \(\displaystyle 0{,}3\) | \(\displaystyle 0{,}4\) | \(\displaystyle 0{,}6\) | \(\displaystyle 0{,}8\) | \(\displaystyle 1\) |
| \(\displaystyle \small y=2x^2\) | \(\displaystyle 2\) | \(\displaystyle 1{,}28\) | \(\displaystyle 0{,}72\) | \(\displaystyle 0{,}32\) | \(\displaystyle 0{,}18\) | \(\displaystyle 0\) | \(\displaystyle 0{,}18\) | \(\displaystyle 0{,}32\) | \(\displaystyle 0{,}72\) | \(\displaystyle 1{,}28\) | \(\displaystyle 2\) |
Жазықтықта нүктелерді салайық:
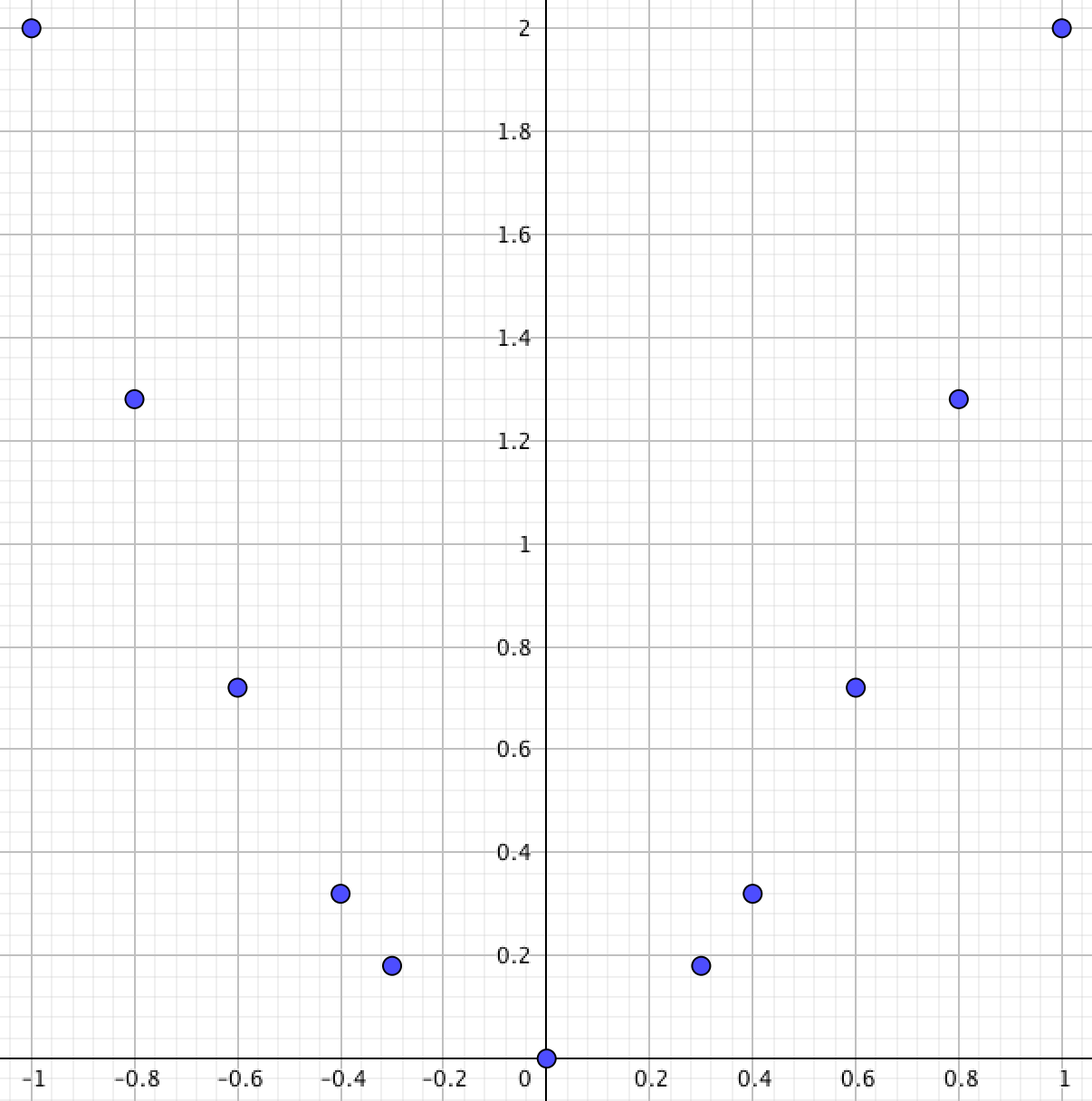
\(\displaystyle y=2x^2\) квадраттық функциясының графигін қажет болған жағдайда тағы да нүктелер қосып, алынған нүктелер бойынша салайық:
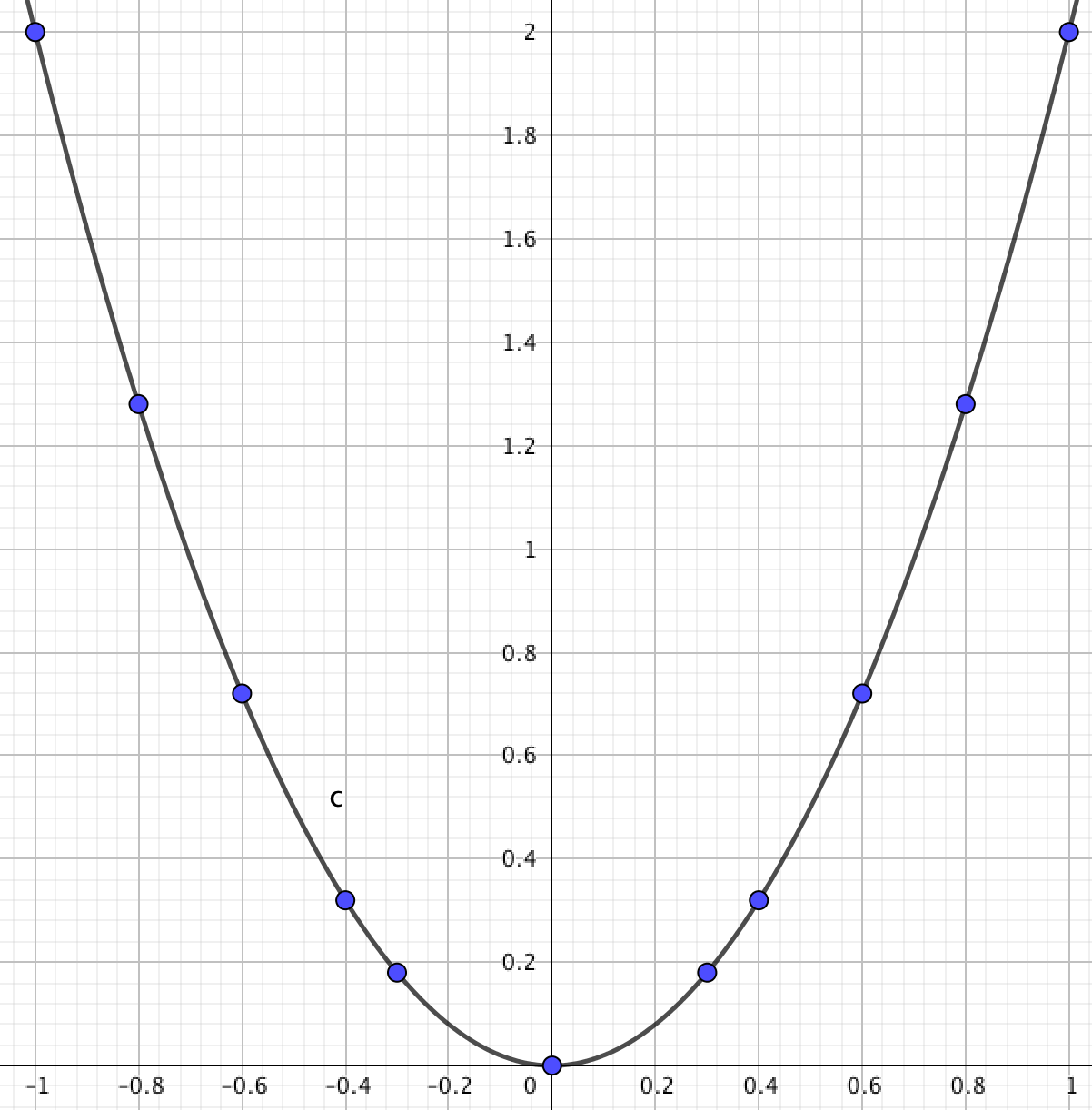
Замечание / комментарий
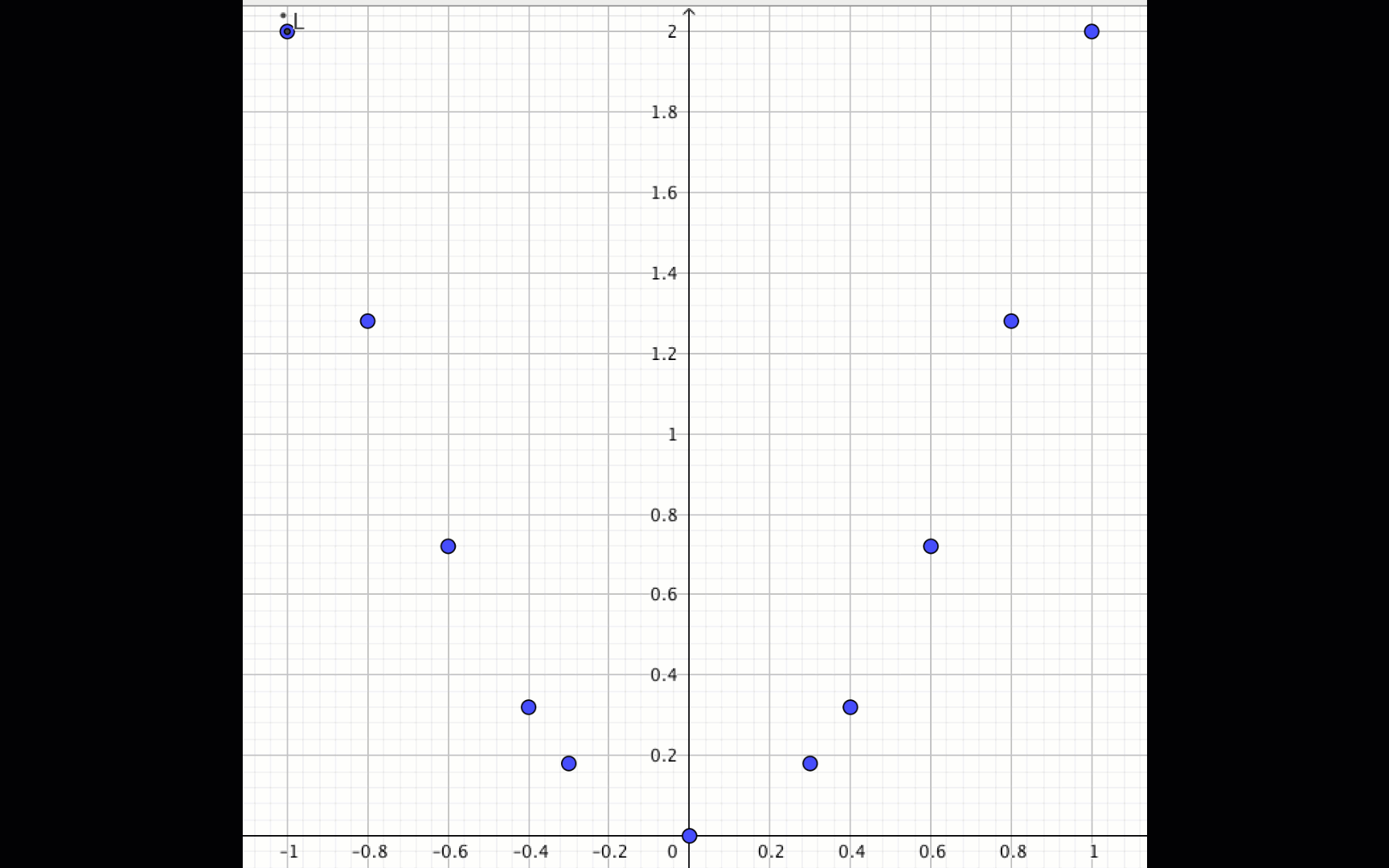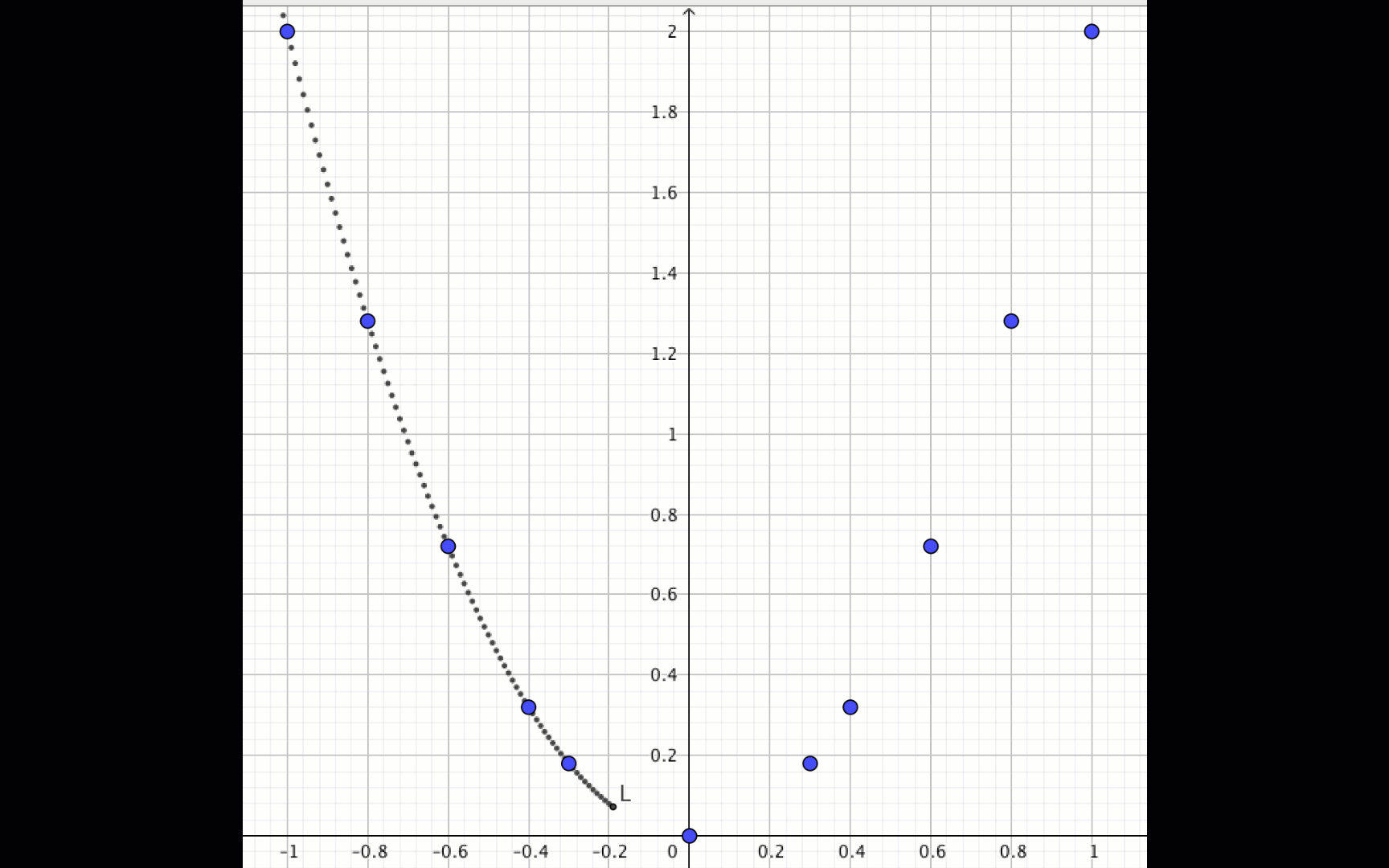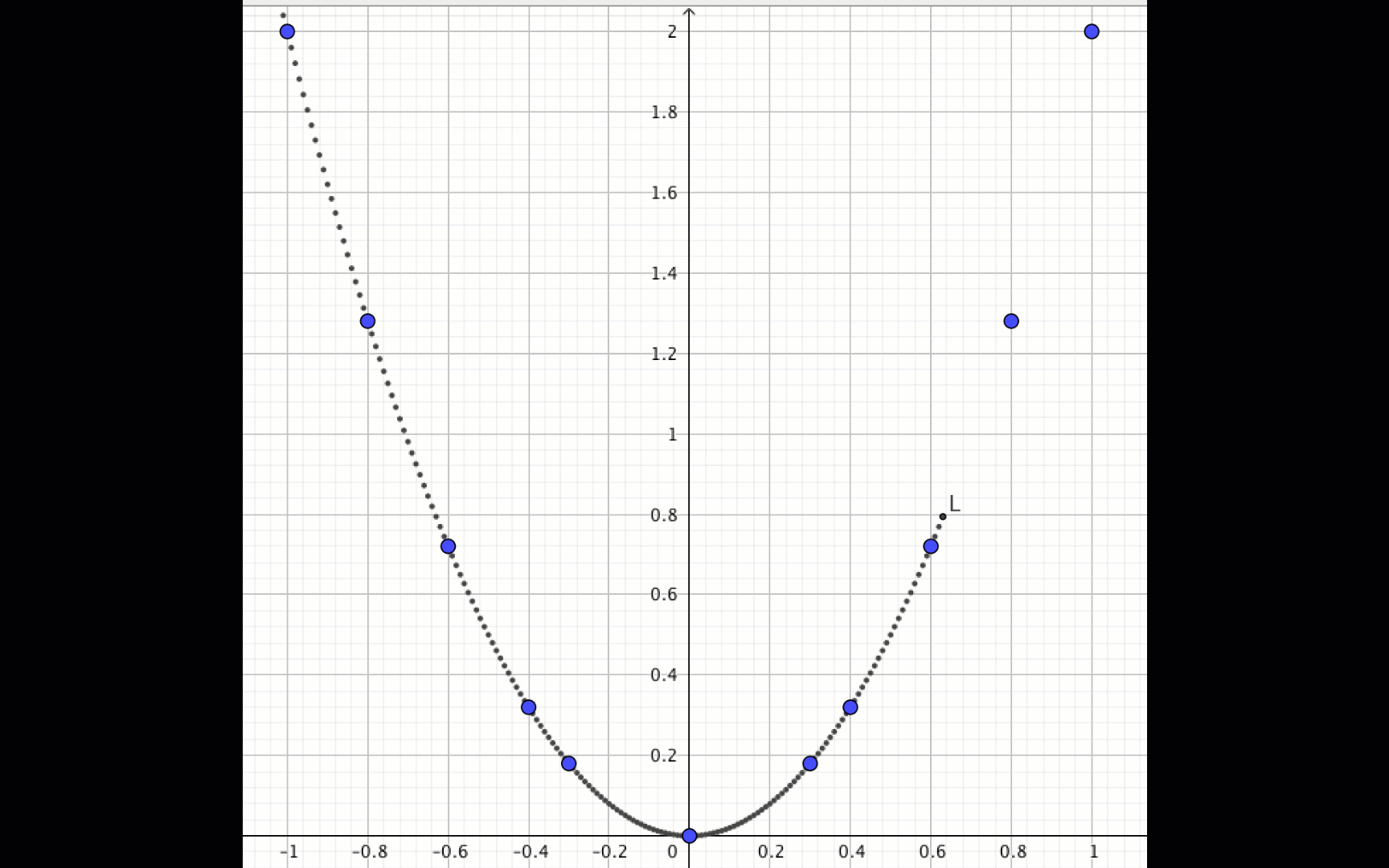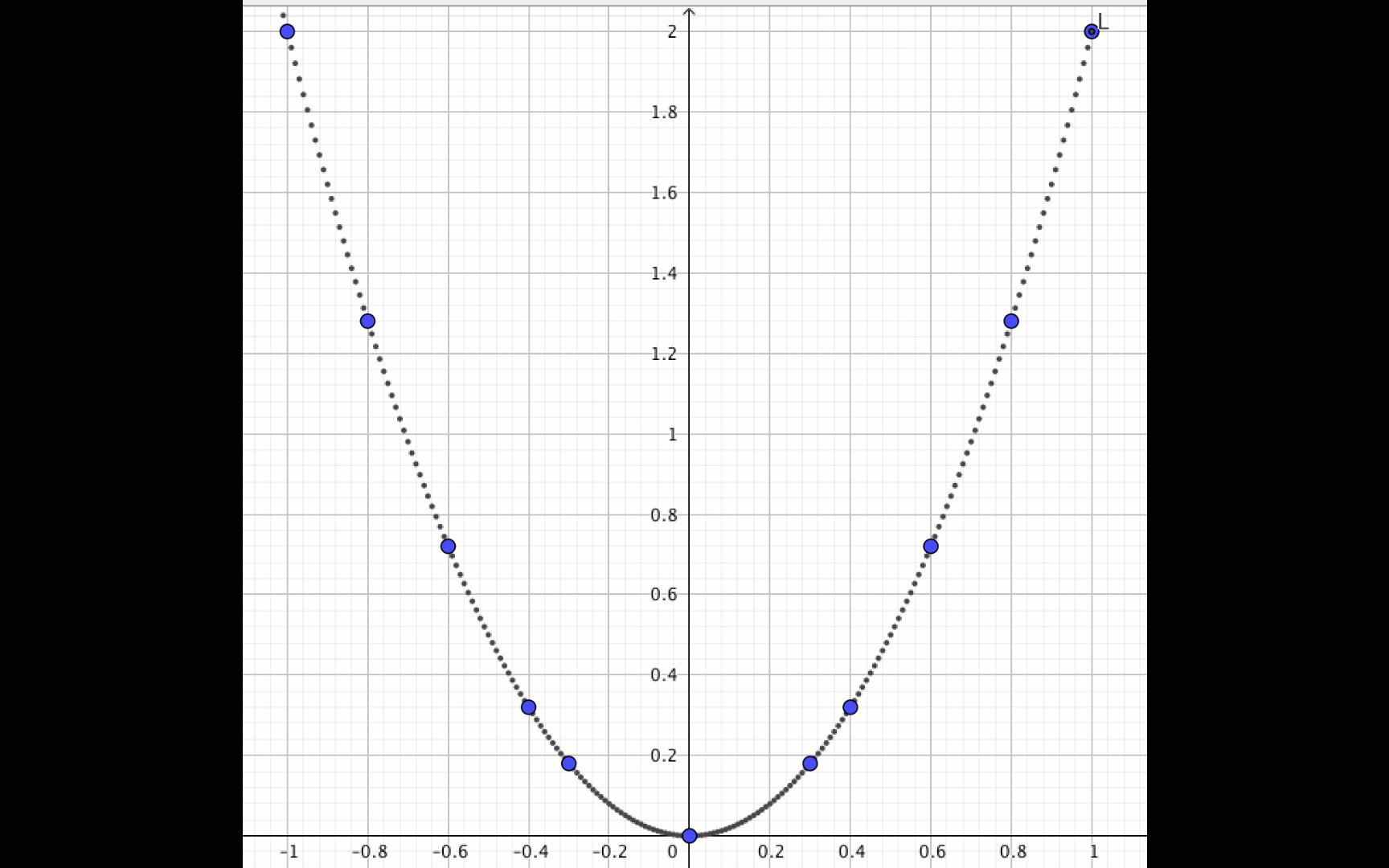
Нүктелер бойынша салу
Егер \(\displaystyle -1 \)-ден \(\displaystyle 1{\small } \) дейінгі координаттары бар OX осі бойымен көптеген нүктелер салсақ, онда біз графиктің келесі суретін аламыз: