Тапсырма
Дұрыс сәйкестікті таңдаңыз:
| \(\displaystyle y=f^{\prime}(x)\) | \(\displaystyle y=f(x)\) |
 | |
 |
Шешім
Ереже
- Егер әрбір нүктеде \(\displaystyle x_0 \in (\alpha; \beta): f^{\prime}(x_0)>0{ \small }\) болса, \(\displaystyle f(x)\) функциясы \(\displaystyle (\alpha; \beta){\small }\) аралығында артады.
- Егер әрбір нүктеде \(\displaystyle x_0 \in (\alpha; \beta): f^{\prime}(x_0)<0{ \small }\) болса, \(\displaystyle f(x)\) функциясы \(\displaystyle (\alpha; \beta){\small }\) аралығында азаяды.
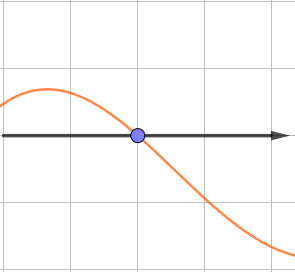
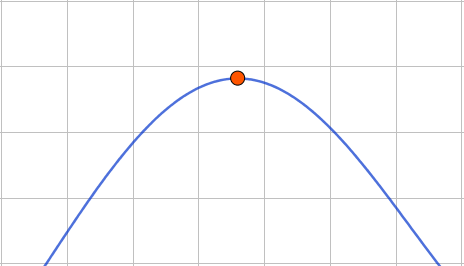
--------Бірінші график---------
\(\displaystyle y=f^{\prime}(x)\) функциясының туындысының бірінші графигінде

қиылысу нүктесіне дейінгі туынды оң, қиылысу нүктесінен кейін теріс.
Демек, қиылысу нүктесіне дейінгі аралықта функция артады, содан кейін азаяды:
| \(\displaystyle y=f^{\prime}(x)\) | \(\displaystyle +\) | қиылысу нүктесі | \(\displaystyle -\) |
| \(\displaystyle y=f(x)\) | \(\displaystyle \nearrow\) | максимум | \(\displaystyle \searrow\) |
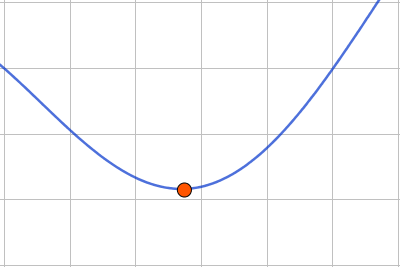
--------Екінші график---------
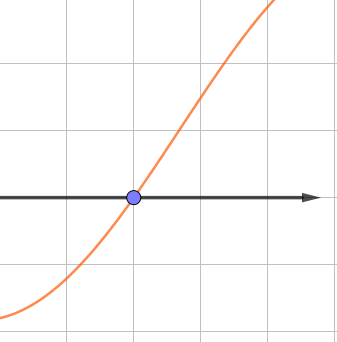
\(\displaystyle y=f^{\prime}(x)\) функциясының туындысының екінші графигінде

қиылысу нүктесіне дейінгі туынды теріс, қиылысу нүктесінен кейін оң болады.
Демек, қиылысу нүктесіне дейінгі аралықта функция азаяды, содан кейін артады:
| \(\displaystyle y=f^{\prime}(x)\) | \(\displaystyle -\) | қиылысу нүктесі | \(\displaystyle +\) |
| \(\displaystyle y=f(x)\) | \(\displaystyle \searrow\) | минимум | \(\displaystyle \nearrow\) |