 | 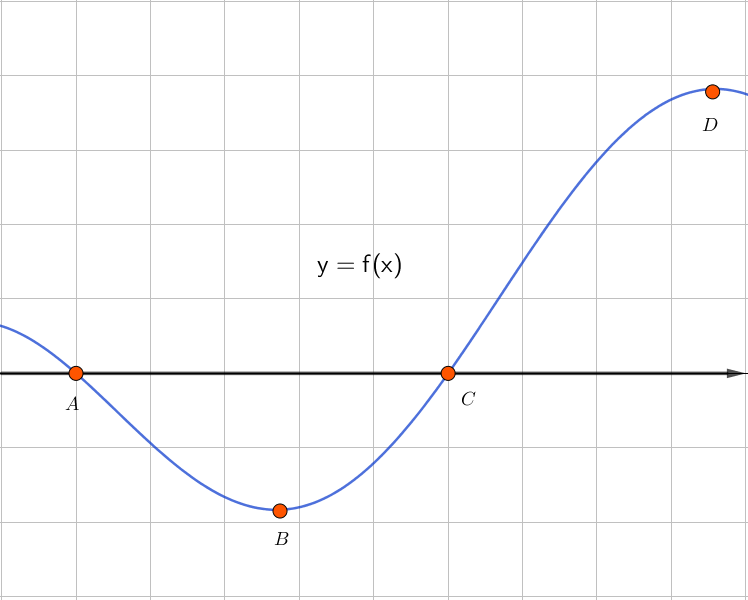 |
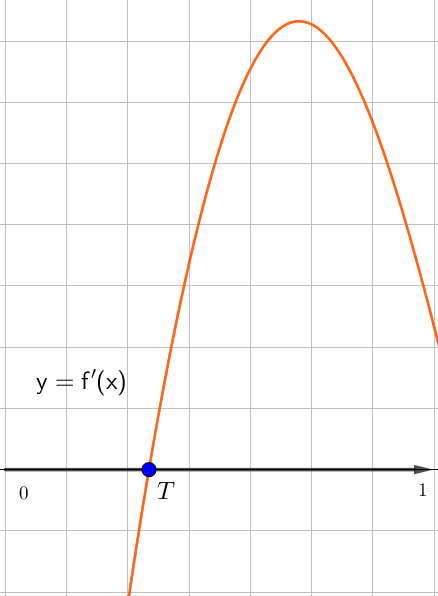
\(\displaystyle y=f(x)\) функциясының графигінің қай нүктесі \(\displaystyle T\) функциясының туындысының графигінің \(\displaystyle y=f^{\prime}(x){\small }\) нүктесіне сәйкес келеді?
- Егер әрбір нүктеде \(\displaystyle x_0 \in (\alpha; \beta): f^{\prime}(x_0)>0{ \small }\) болса, \(\displaystyle f(x)\) функциясы \(\displaystyle (\alpha; \beta){\small }\) аралығында артады.
- Егер әрбір нүктеде \(\displaystyle x_0 \in (\alpha; \beta): f^{\prime}(x_0)<0{ \small }\) болса, \(\displaystyle f(x)\) функциясы \(\displaystyle (\alpha; \beta){\small }\) аралығында азаяды.
Туынды теріс болатын аралық
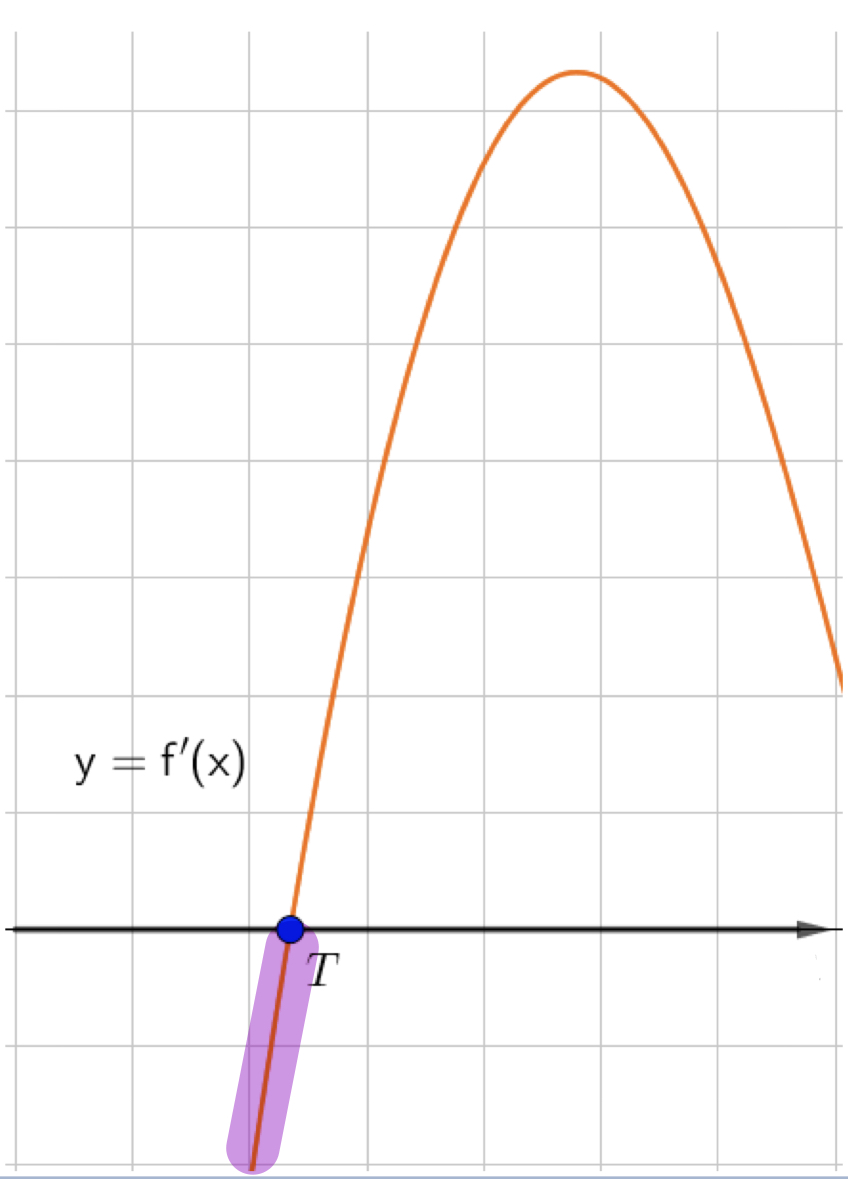
кемімелі функция аралығына сәйкес келеді:
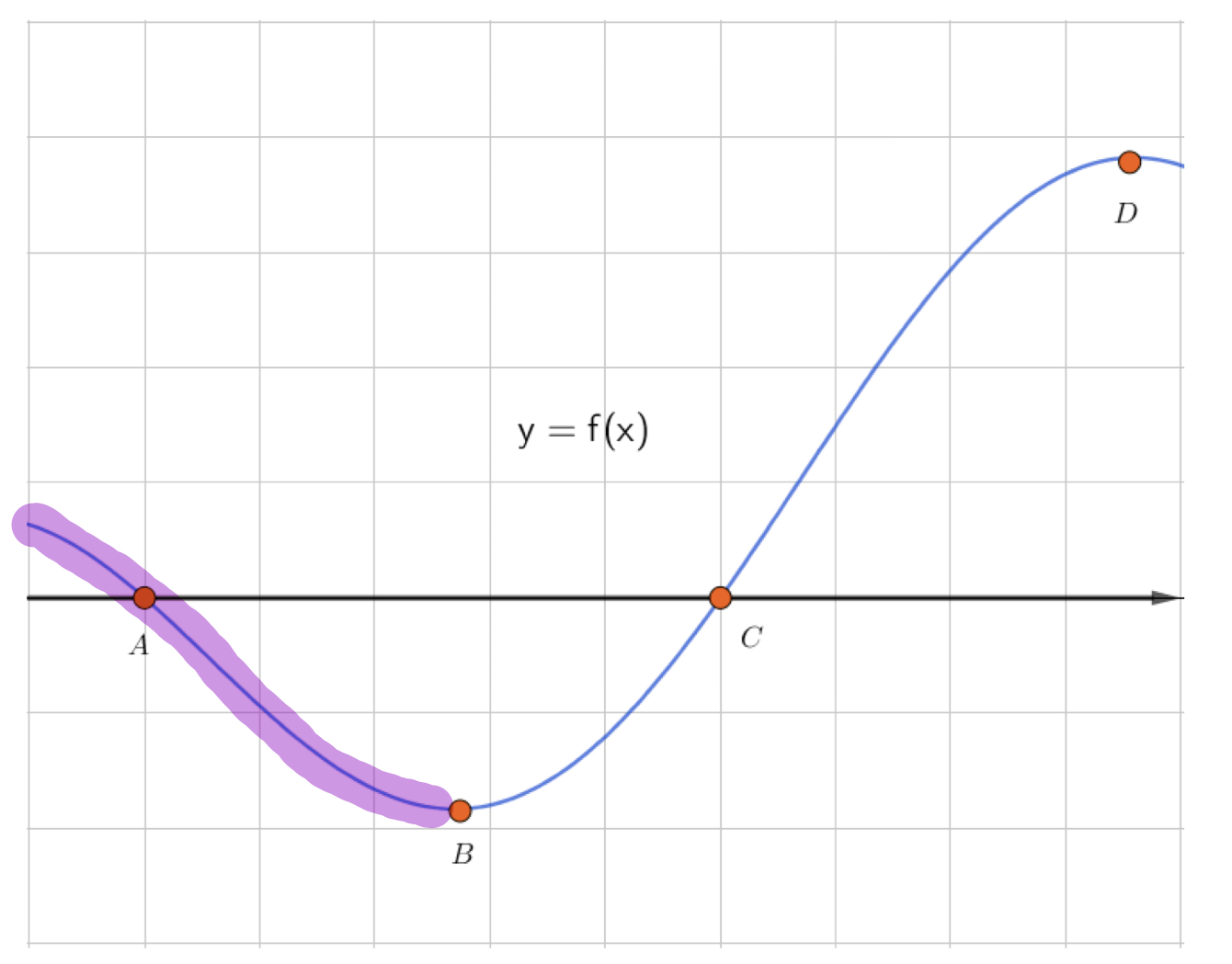
Туынды оң болатын интервал
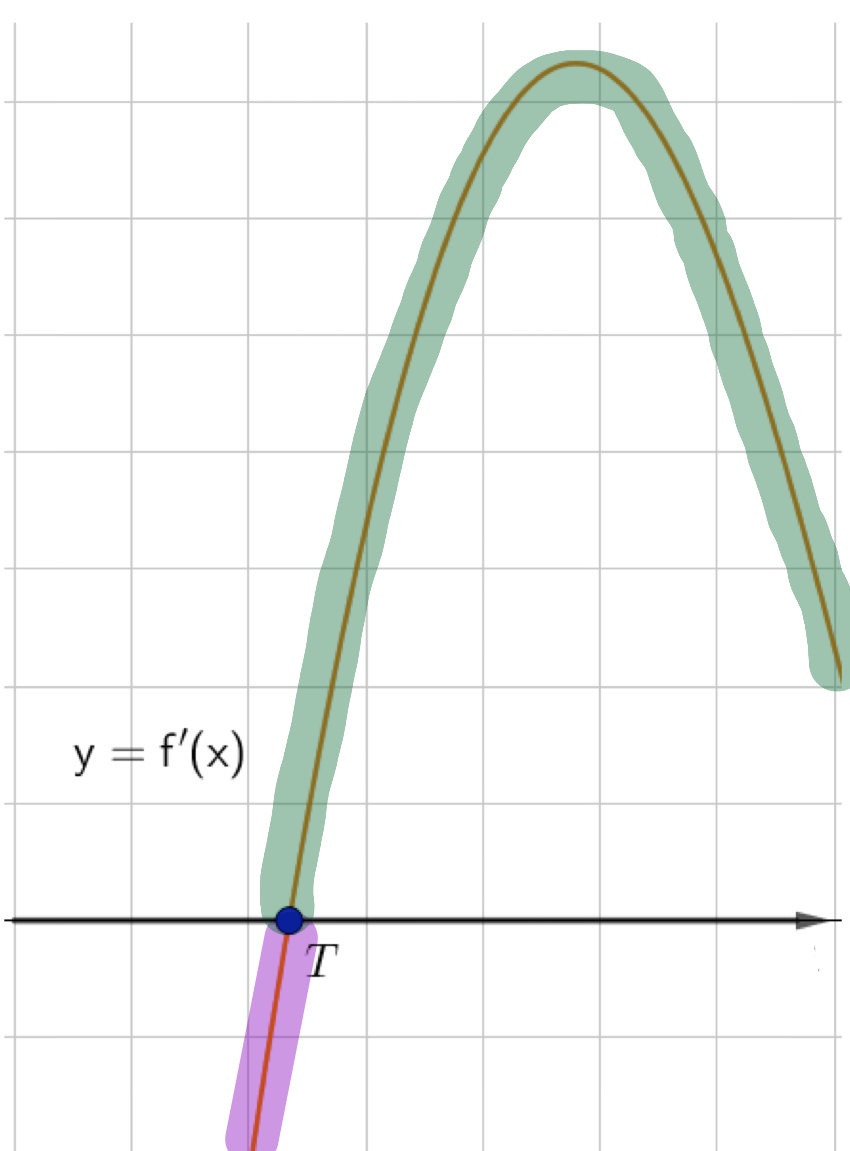
өсу функциясының аралығына сәйкес келеді:
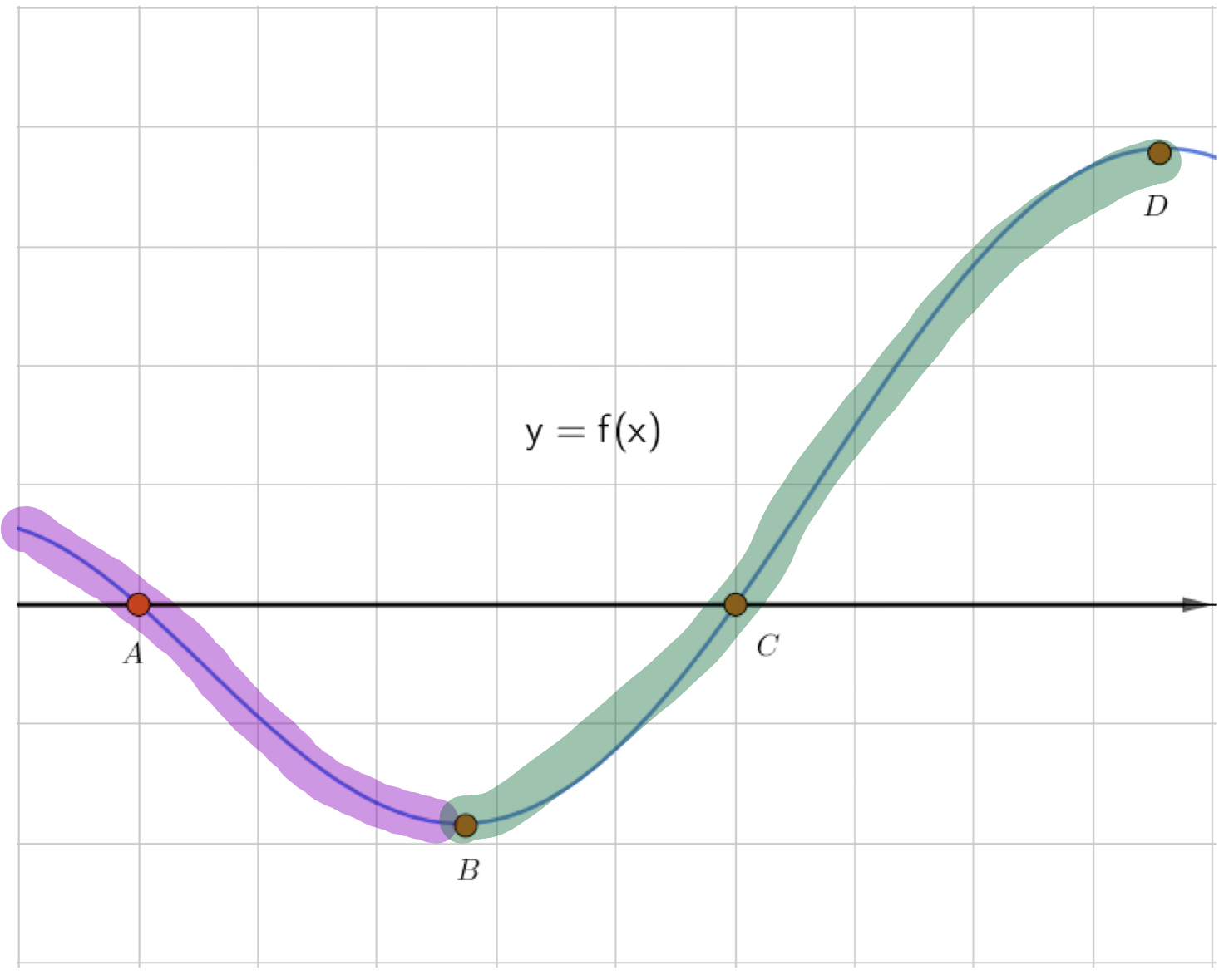
Сонымен, графиктің \(\displaystyle T\) нүктесі \(\displaystyle y=f^{\prime}(x)\) функцияның жергілікті минималды нүктесіне сәйкес келед \(\displaystyle y=f(x){ \small }\) нүктесі \(\displaystyle B{\small .}\)
Жауабы: нүкте \(\displaystyle B{\small .}\)