 | |
 |
Выберите график производной функции, соответствующий участку графика функции.
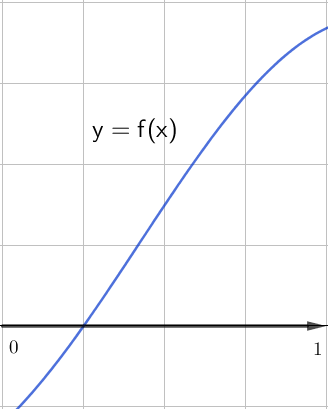
На первом графике функции

функция возрастает и, следовательно, \(\displaystyle f^{\prime}(x)\ge 0\) на данном промежутке. На данном промежутке нет касательных, параллельных оси \(\displaystyle \rm OX{ \small ,}\) то есть нет точек, для которых \(\displaystyle f^{\prime}(x)=0{\small .}\)
Поэтому на данном промежутке \(\displaystyle f^{\prime}(x)>0{\small .}\)
Из представленных двух графиков
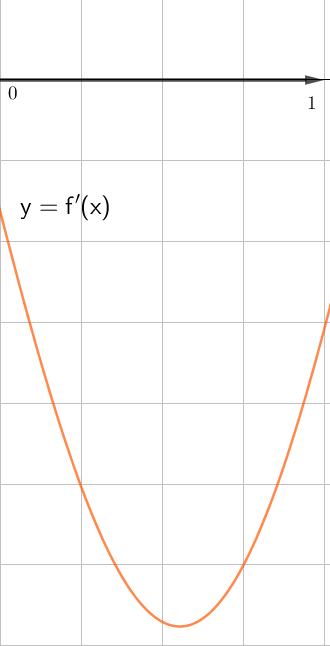 | 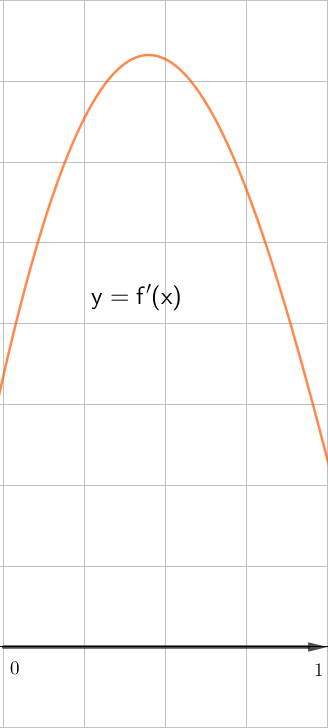 |
выбираем тот, который лежит выше оси \(\displaystyle \rm OX{\small :}\)
 | 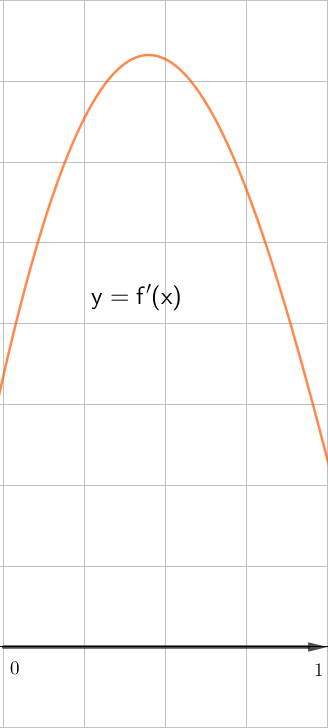 |
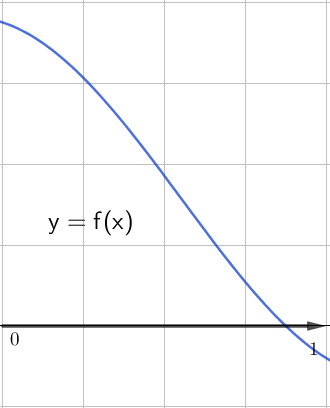
На втором графике функции

функция убывает и, следовательно, \(\displaystyle f^{\prime}(x)\le 0\) на данном промежутке. На данном промежутке нет касательных, параллельных оси \(\displaystyle \rm OX{ \small ,}\) то есть нет точек, для которых \(\displaystyle f^{\prime}(x)=0{\small .}\)
Поэтому на данном промежутке \(\displaystyle f^{\prime}(x)<0{\small .}\)
Из представленных двух графиков
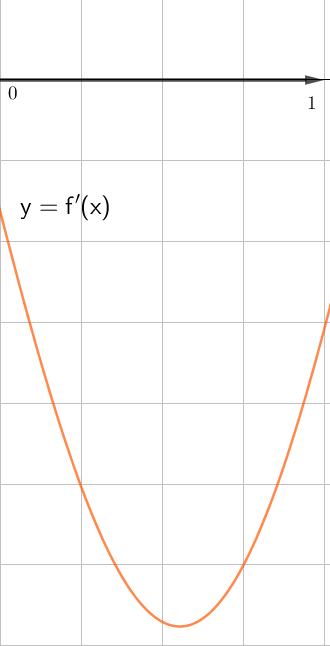 | 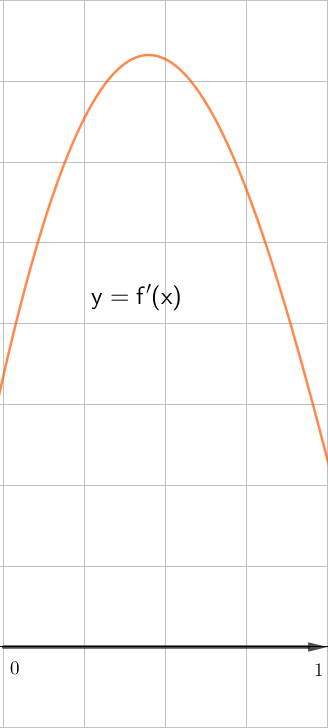 |
выбираем тот который лежит ниже оси \(\displaystyle \rm OX{\small :}\)
 | 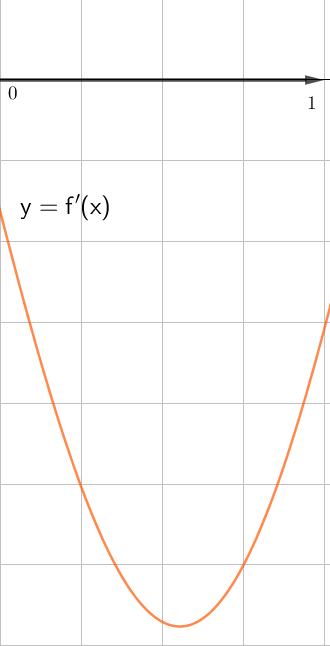 |