 | |
 |
Функцияның туындысының учаскесіне сәйкес функцияның графигін таңдаңыз.
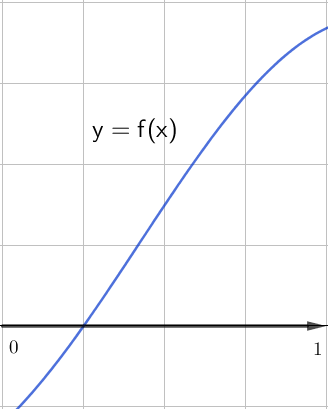
Функцияның бірінші графигінде

функция артады, демек \(\displaystyle f^{\prime}(x)\ge 0\) берілген аралықта. Бұл аралықта \(\displaystyle \rm OX{ \small }\) оське параллель жанамалар жоқ, яғни \(\displaystyle f^{\prime}(x)=0{\small}\) болатын нүктелер жоқ.
Сондықтан осы аралықта \(\displaystyle f^{\prime}(x)>0{\small .}\)
Екі графиктен
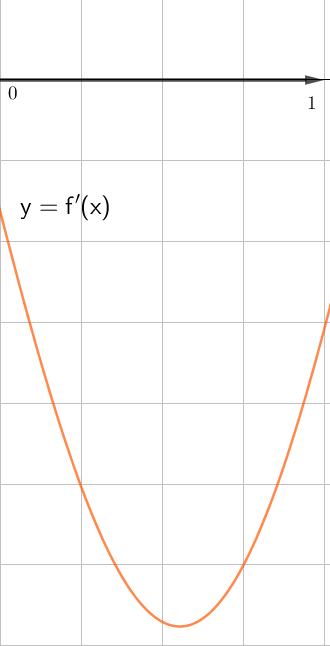 | 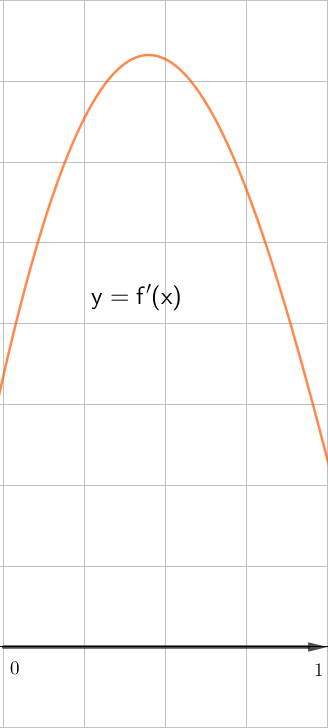 |
осінен \(\displaystyle \rm OX{\small }\) жоғары орналасқанын таңдаңыз:
 | 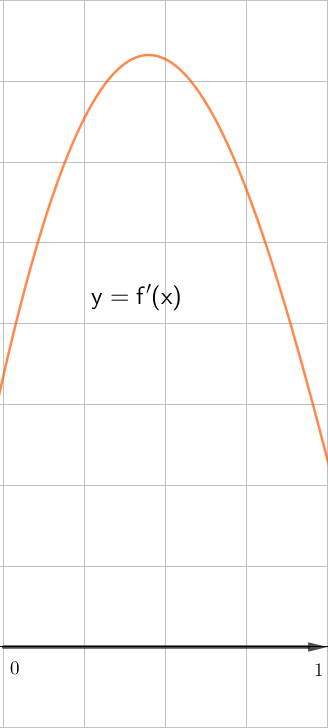 |
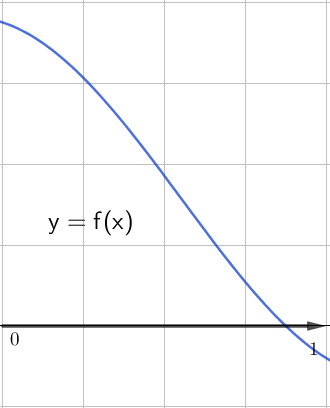
Функцияның екінші графигінде

функция кемиді, демек, \(\displaystyle f^{\prime}(x)\le 0\) берілген аралықта. Бұл аралықта \(\displaystyle \rm OX{ \small }\) оське параллель жанамалар жоқ, яғни \(\displaystyle f^{\prime}(x)=0{\small}\) болатын нүктелер жоқ.
Демек, осы аралықта \(\displaystyle f^{\prime}(x)<0{\small .}\)
Екі графиктен
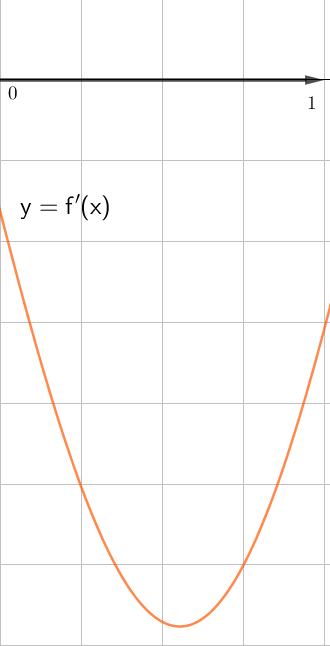 | 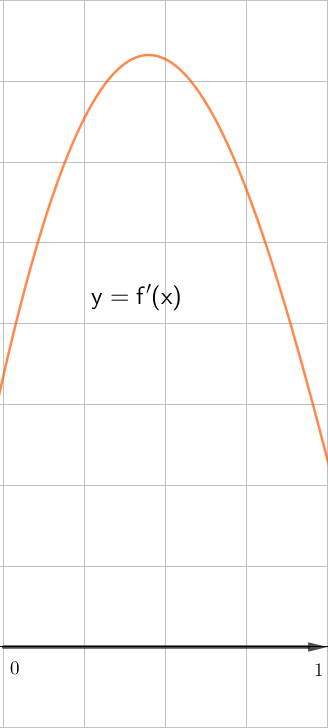 |
осінен \(\displaystyle \rm OX{\small}\) төмен орналасқанын таңдаңыз
 | 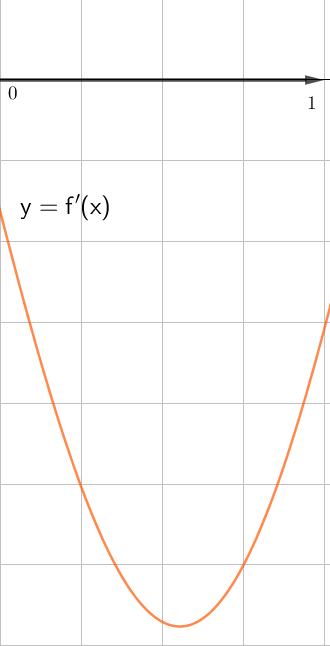 |