\(\displaystyle \cos\left(\frac{6\pi}{5}\right)\) және \(\displaystyle \sin \left(\frac{6\pi}{5}\right){\small}\) таңбаларын анықтаңыз.
\(\displaystyle \cos \left(\frac{6\pi}{5}\right)\) и \(\displaystyle \sin\left(\frac{6\pi}{5}\right)\)
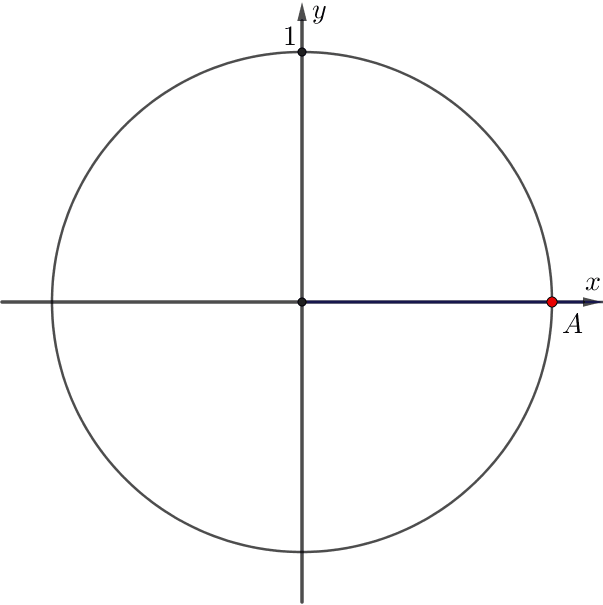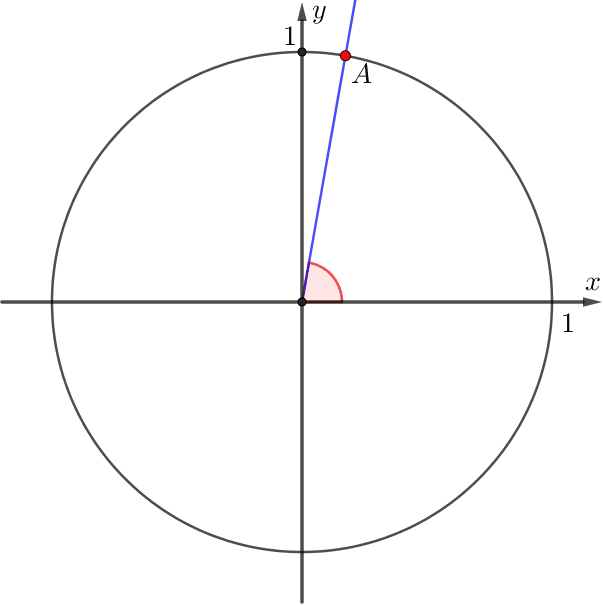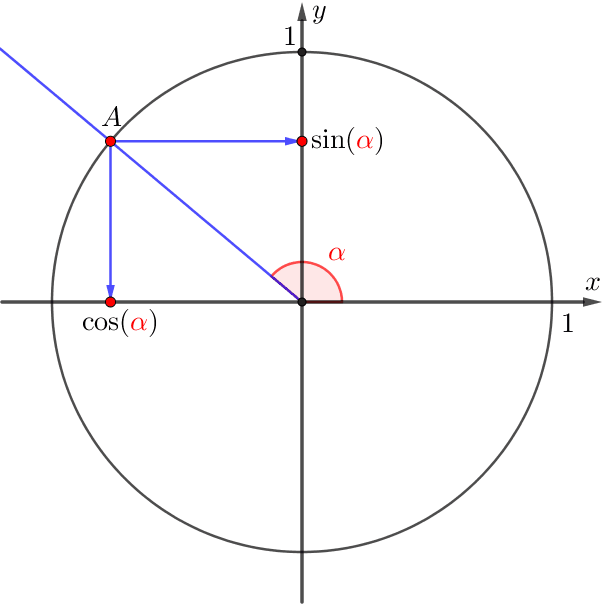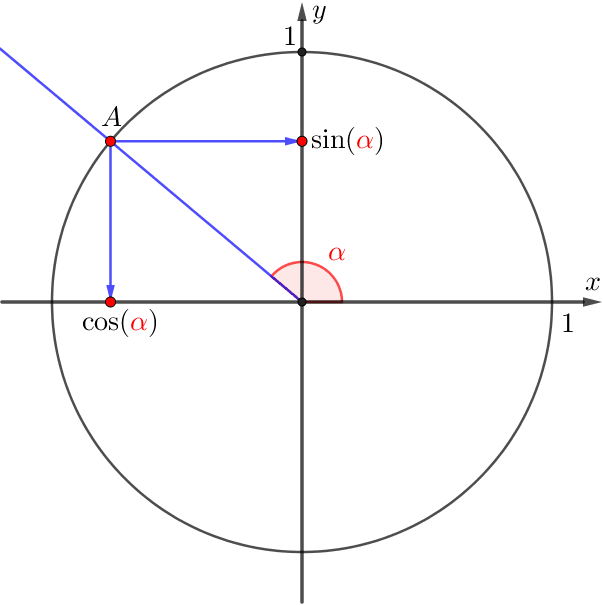
Бұрыштың синусы мен косинусының анықтамасын қолданамыз.
Сонда \(\displaystyle \cos\left(\frac{6\pi}{5}\right)\) және \(\displaystyle \sin \left(\frac{6\pi}{5}\right)\) – сәуленің \(\displaystyle \frac{6\pi}{5}{\small} \) бұрышқа бұрылуынан алынған нүктелерінің координаталары.
Бұл ретте \(\displaystyle \frac{6\pi}{5}=\pi+\frac{\pi}{5}{ \small } \) болғандықтан, \(\displaystyle OA\) сәулесі \(\displaystyle \rm III\) ширекте болады:
Демек, \(\displaystyle A\) нүктесінің абсциссасы мен ординатасы теріс.
Демек,
- \(\displaystyle \cos\left(\frac{6\pi}{5}\right)<0{\small,}\)
- \(\displaystyle \sin\left(\frac{6\pi}{5}\right)<0{\small.}\)
Жауабы: \(\displaystyle \cos\left(\frac{6\pi}{5}\right)<0\) және \(\displaystyle \sin \left(\frac{6\pi}{5}\right)<0{\small.}\)