\(\displaystyle A{\small} \) нүктесі белгіленген бірлік шеңбер берілген. \(\displaystyle A{\small} \) нүктесінің координаталарын анықтаңыз.
\(\displaystyle A\) нүктесінің абсциссасы
\(\displaystyle A\) нүктесінің ординатасы
Центрі \(\displaystyle O{\small}\) нүктесінде болатын бірлік шеңбер берілген. \(\displaystyle A\) нүктесі \(\displaystyle (1;0){\small }\) координаталарына ие.
\(\displaystyle OA\) сәулесі \(\displaystyle \color{red}{\alpha}{\small}\) бұрышына бұрылды.
Сонда
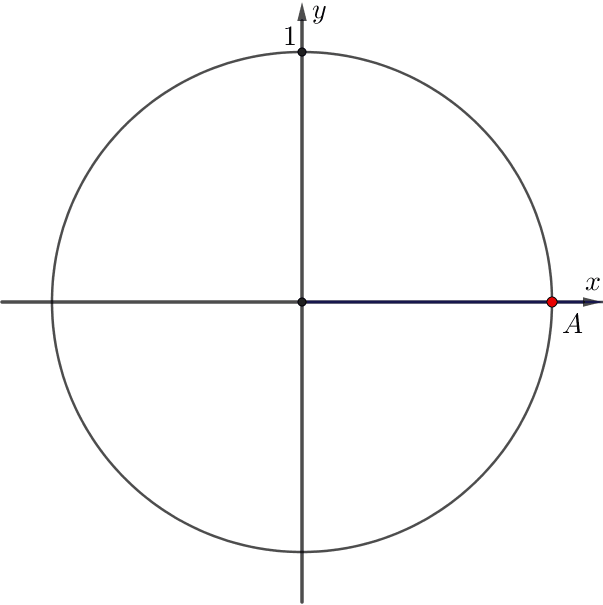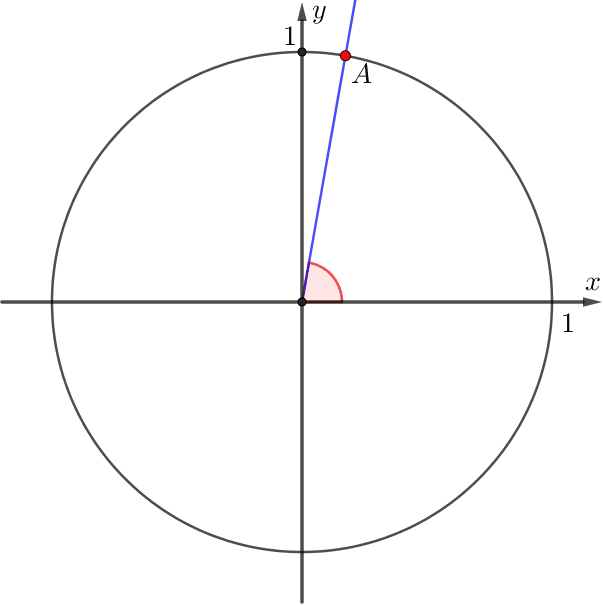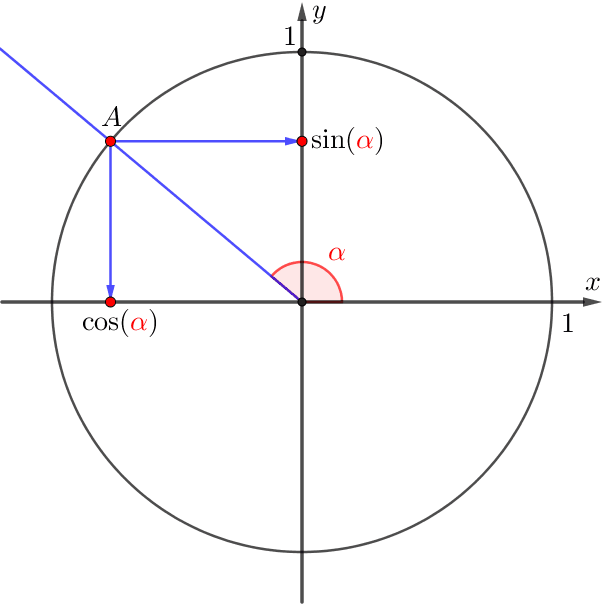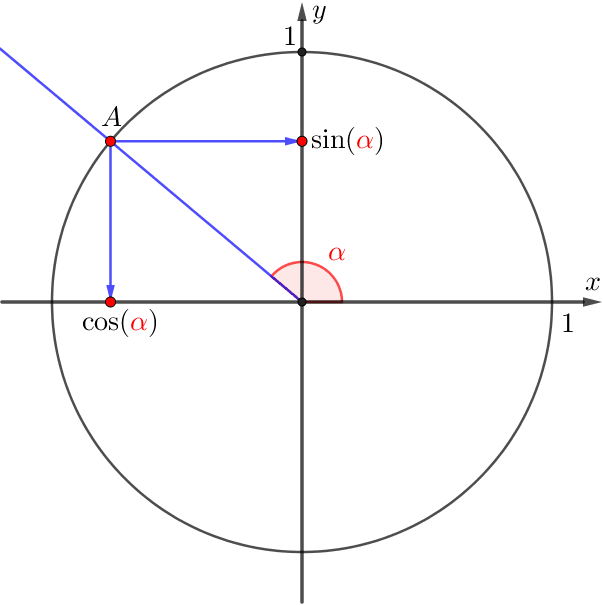
- \(\displaystyle \color{red}{\alpha}\) бұрышының косинусы деп \(\displaystyle A\) нүктесінің абциссасы аталады және \(\displaystyle \cos(\color{red}{\alpha}){\small}\) арқылы белгіленеді.
- \(\displaystyle \color{red}{\alpha}\) бұрышының синусы деп \(\displaystyle A\) нүктесінің ординатасы аталады және \(\displaystyle \sin(\color{red}{\alpha}){\small}\) арқылы белгіленеді.
Шартта ұсынылған суретте \(\displaystyle \rm OX\) осінің оң бағыты мен \(\displaystyle OA\) сәулесінің арасындағы бұрыш \(\displaystyle \frac{13\pi}{11}{\small}\) тең.
Демек, \(\displaystyle A\) нүктесінің абсциссасы \(\displaystyle \cos\left(\frac{13\pi}{11}\right){\small}\) тең, \(\displaystyle A\) нүктесінің ординатасы \(\displaystyle \sin\left(\frac{13\pi}{11}\right){\small}\) тең. |