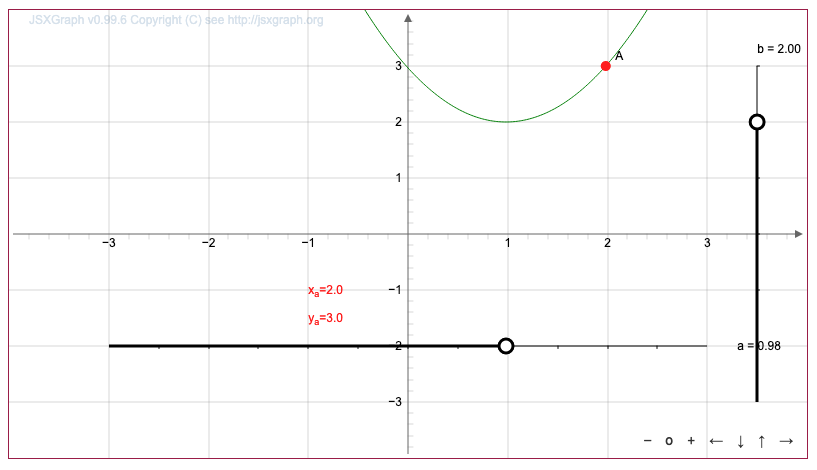
Функцияның \(\displaystyle y=x^2{\small }\) графигі берілген Функцияның \(\displaystyle y=(x-1)^2+2\) графигін салыңыз
және нүктенің координаталарын табыңыз
\(\displaystyle A=(\)\(\displaystyle ;\) \(\displaystyle )\)
ондыққа дейін дәл.
\(\displaystyle a\) және \(\displaystyle b\) параметрлерін сырғытпалармен жүздік дәлдікке өзгерту арқылы графикті жылжытыңыз.
Параболадан \(\displaystyle y=x^2\) функциясының графигін алу қажет \(\displaystyle y=(x-1)^2+2{\small .}\)
Оңға \(\displaystyle 1\) бірлікке жылжу аламыз: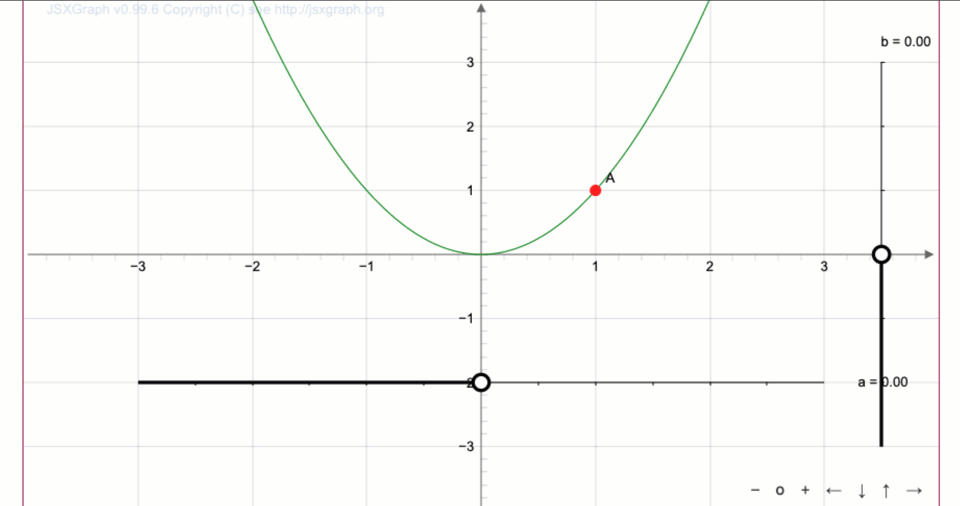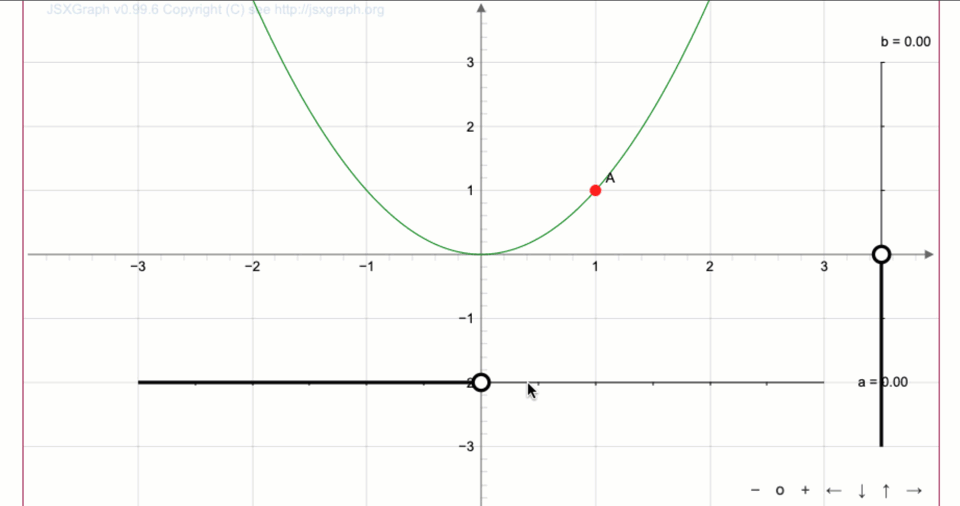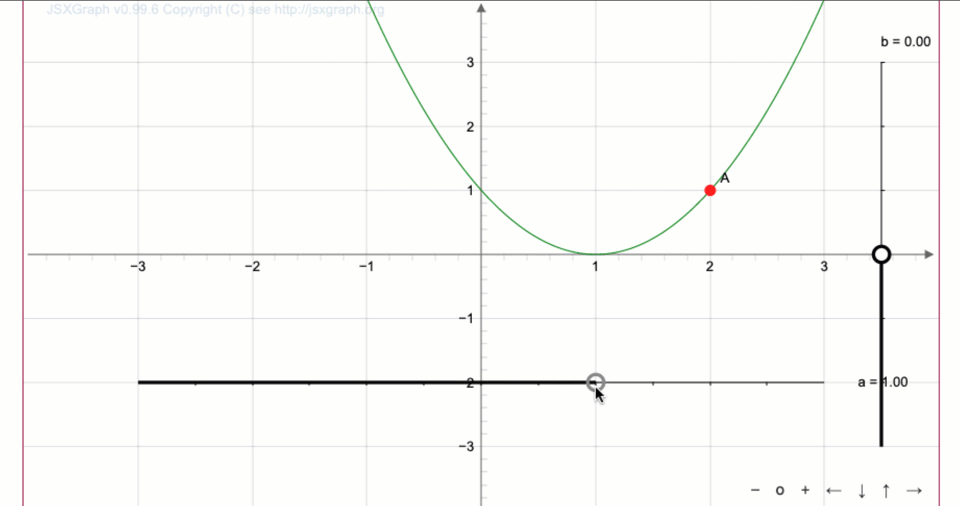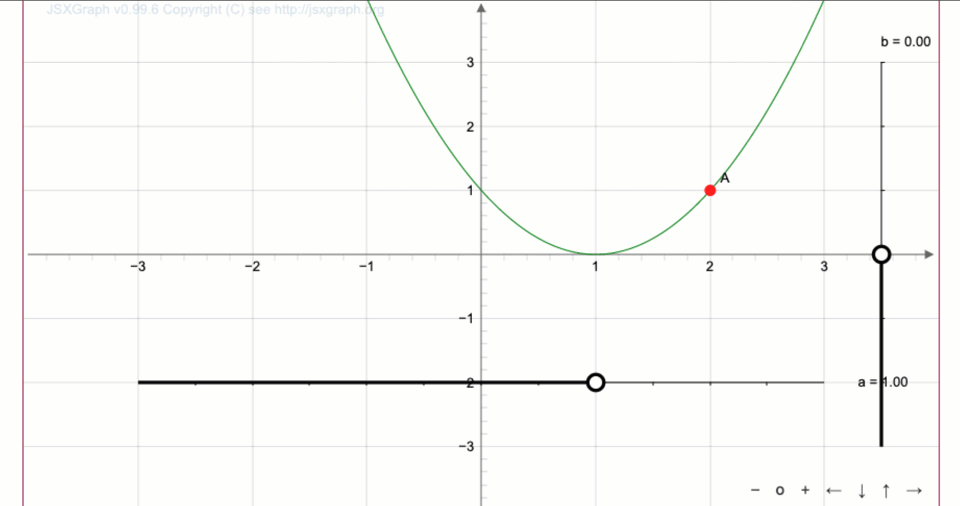
- Егер \(\displaystyle y=f(x) \) функциясының графигі \(\displaystyle \color{blue}{\rm A} \) бірлікке жоғары жылжытылса \(\displaystyle y=f(x){\bf+}\color{blue}{\rm A}{\small } \) функциясының графигін аламыз.
- Егер \(\displaystyle y=f(x) \) функциясының графигі \(\displaystyle \color{blue}{\rm A} \) бірлікке төмен жылжытылса \(\displaystyle y=f(x){\bf-}\color{blue}{\rm A}{\small } \) функциясының графигін аламыз.
Біз \(\displaystyle 2\) бірлік жоғары жылжу аламыз:
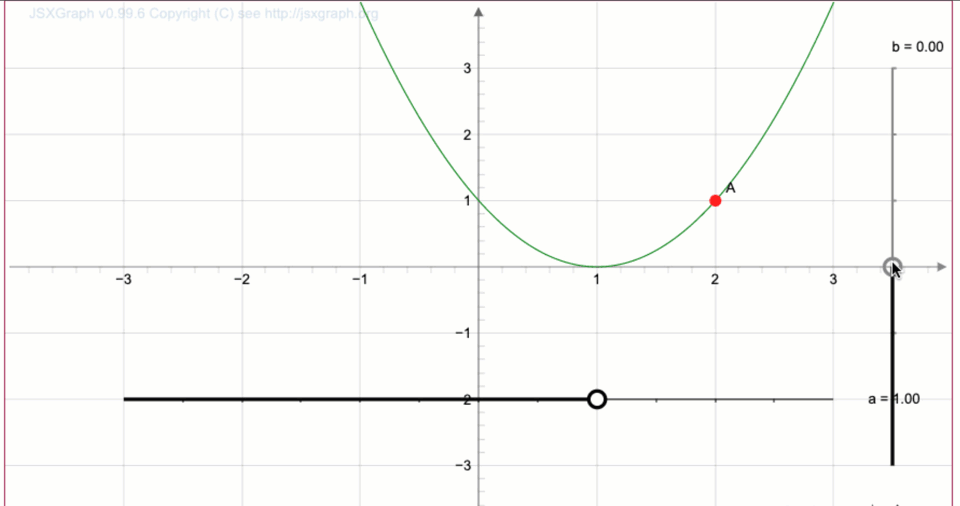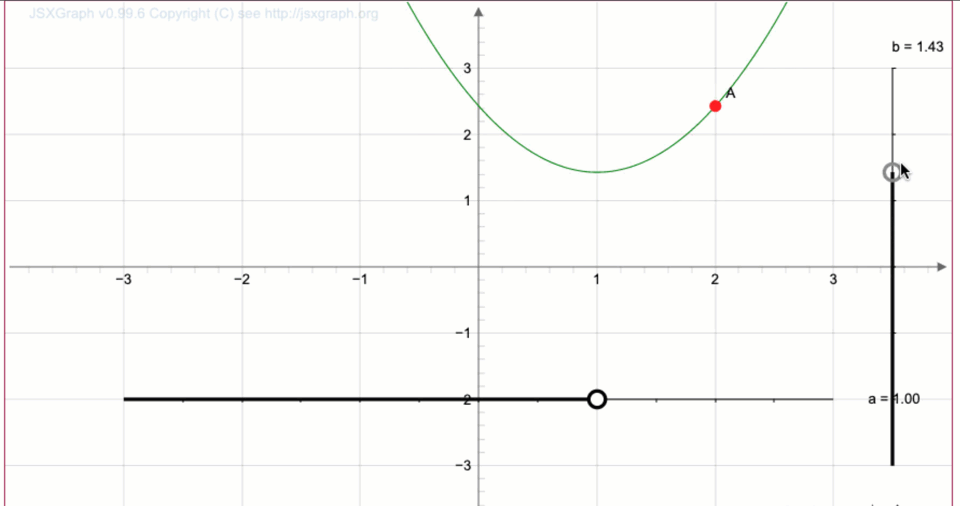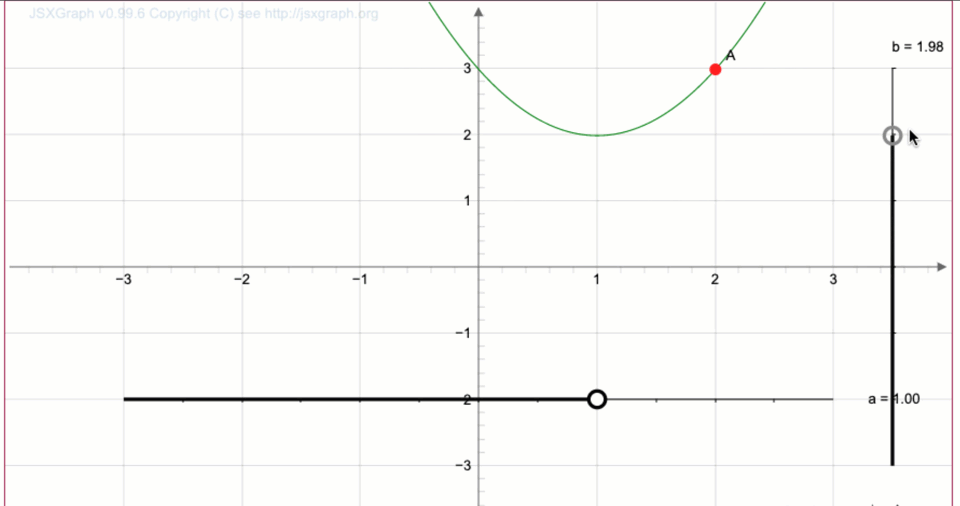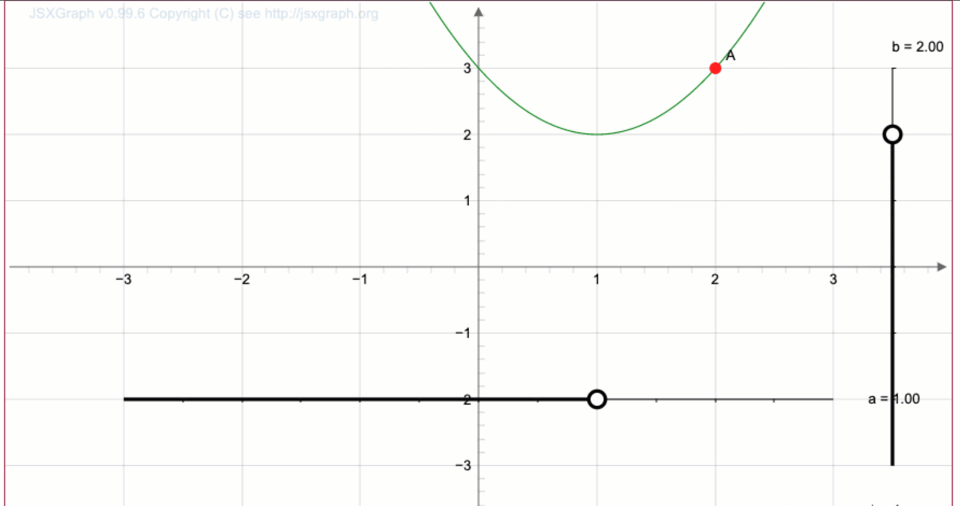
Тінтуір меңзерін нүктенің үстіне апару арқылы біз координаталарды аламыз

Ондыққа дейін дөңгелектегеннен кейін координаталарды аламыз \(\displaystyle (2;\,3){\small .}\)
Жауабы: \(\displaystyle A=(2;\,3){\small .}\)