\(\displaystyle ABCD\) – ромб, \(\displaystyle O\) – оның диагональдары \(\displaystyle AC\) және \(\displaystyle BD{\small}\) қиылысу нүктесі. \(\displaystyle AO{\small}\) кесіндісінің ұзындығын табыңыз, егер ромбтың қабырғасы \(\displaystyle 2\sqrt{3}\) және \(\displaystyle \angle BAO=30^{\circ}{\small.}\)
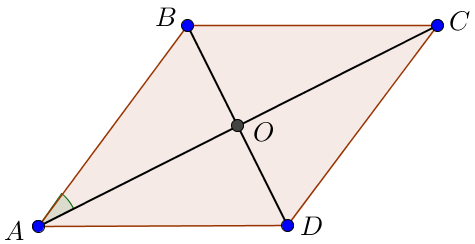

Ромбта диагональдар перпендикуляр болғандықтан \(\displaystyle AOB\) бұрышы тік болады.
Тік бұрышты \(\displaystyle AOB {\small}\) үшбұрышын қарастырайық
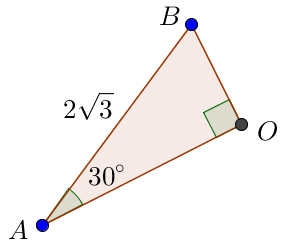
\(\displaystyle 30^{\circ}\) болатын сүйір бұрышы бар тікбұрышты үшбұрышта \(\displaystyle 30^{\circ}{\small,}\) бұрышына қарсы жатқан катет гипотенузаның жартысына тең. Яғни,
\(\displaystyle OB=\frac{1}{2}\cdot AB=\frac{1}{2}\cdot 2\sqrt{3}=\sqrt{3}.\)
Пифагор теоремасы бойынша
\(\displaystyle AB^2=AO^2+OB^2.\)
Демек
\(\displaystyle (2\sqrt{3})^2=AO^2+\left({\sqrt{3}}\right)^2,\)
\(\displaystyle 12=AO^2+{3},\)
\(\displaystyle AO^2=12-3=9.\)
Кесіндінің ұзындығы оң болғандықтан, онда
\(\displaystyle AO=\sqrt{9}={3}.\)
Жауабы: \(\displaystyle 3{\small .}\)