Тапсырма
Ереже
\(\displaystyle a,\, b\) және \(\displaystyle c\) кез келген сандары үшін
\(\displaystyle a-(b-c)=a-b+c{\small }\) екендігі рас
Шешім
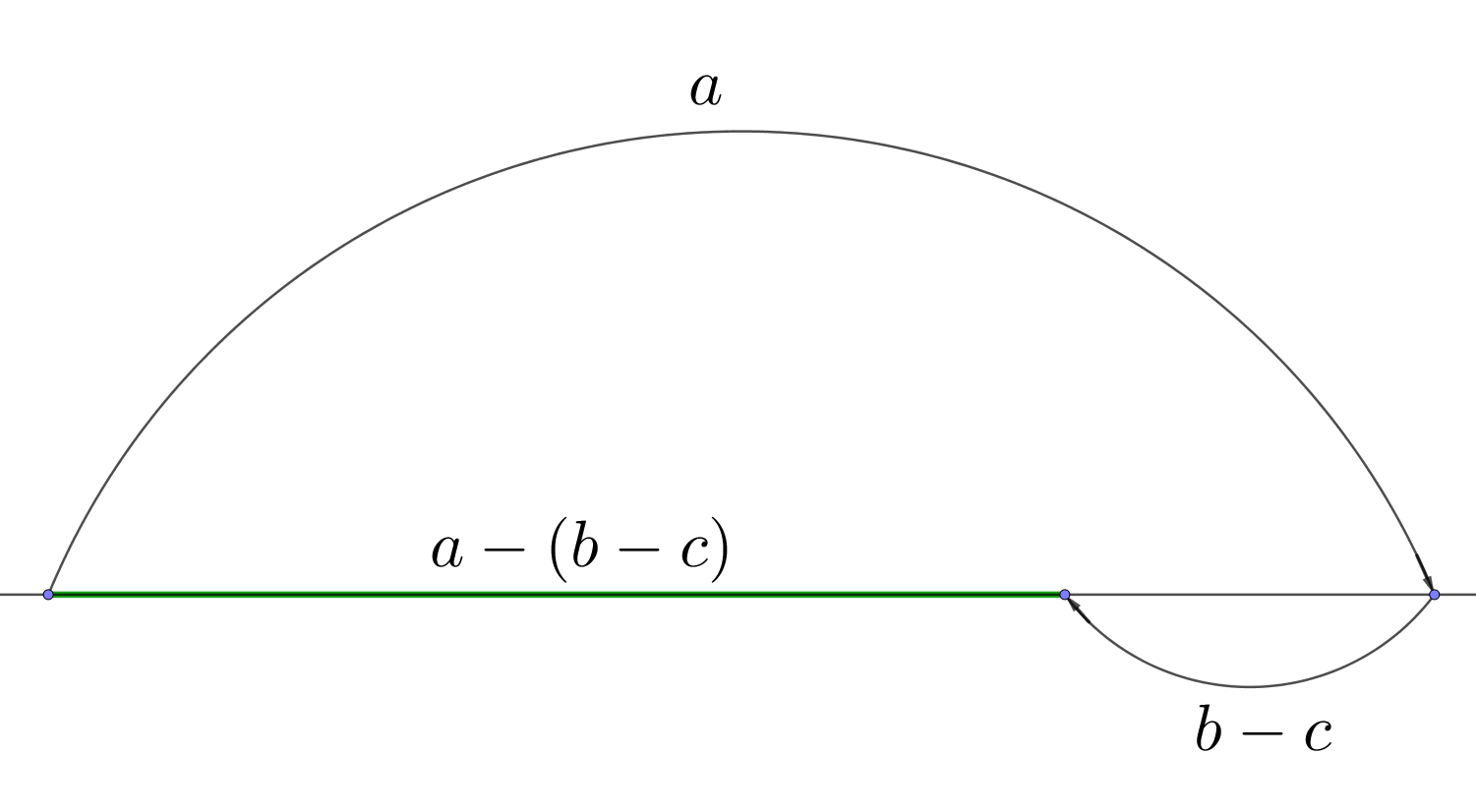
\(\displaystyle a-(b-c)\) кесіндісінің ұзындығын құру

Диаграммада \(\displaystyle a-(b-c){\small }\) кесіндісі ұзындығының құрылуы көрсетілген.
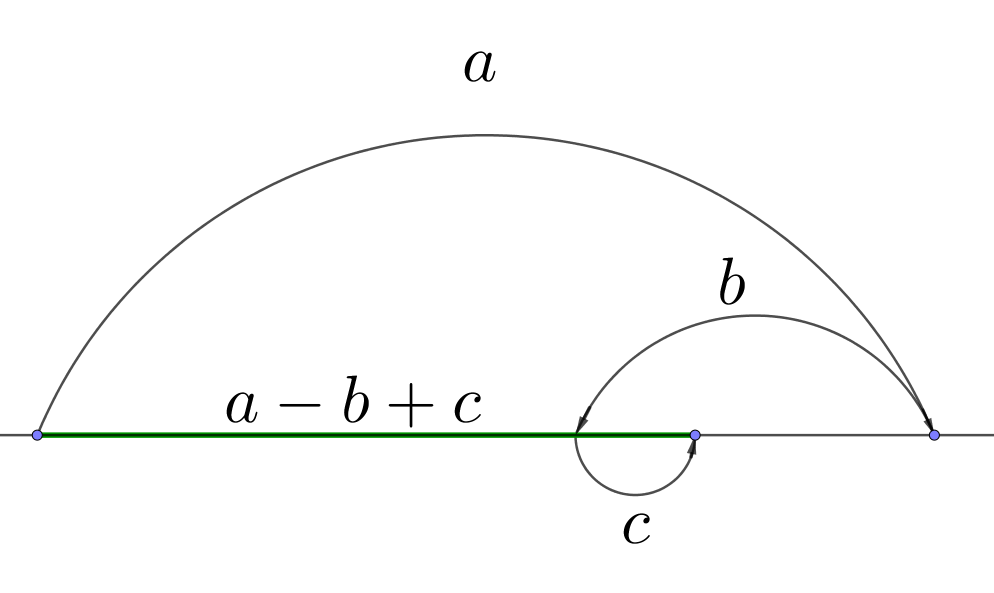
\(\displaystyle a-b+c\) кесіндісінің ұзындығын құру
Замечание / комментарий
\(\displaystyle b-c\) кесіндісін құрудың екі жолы

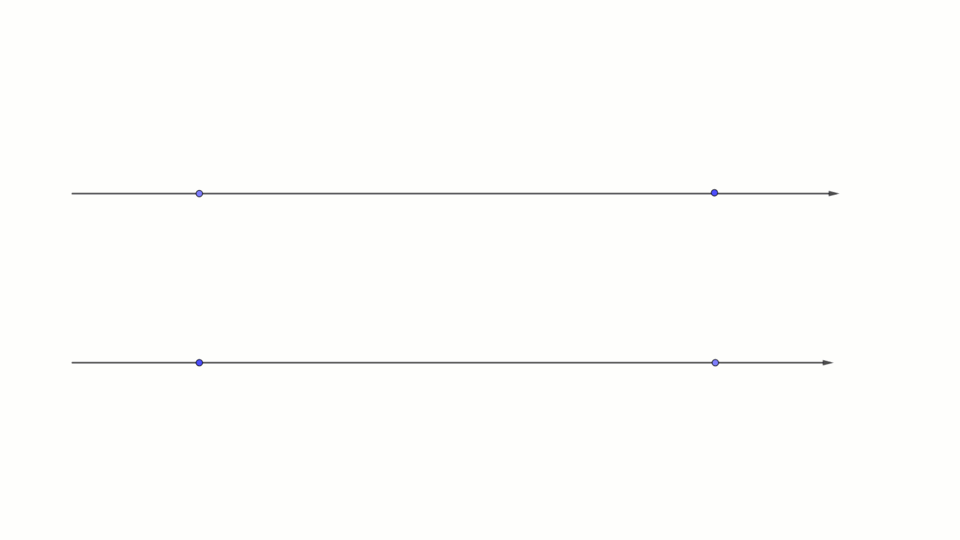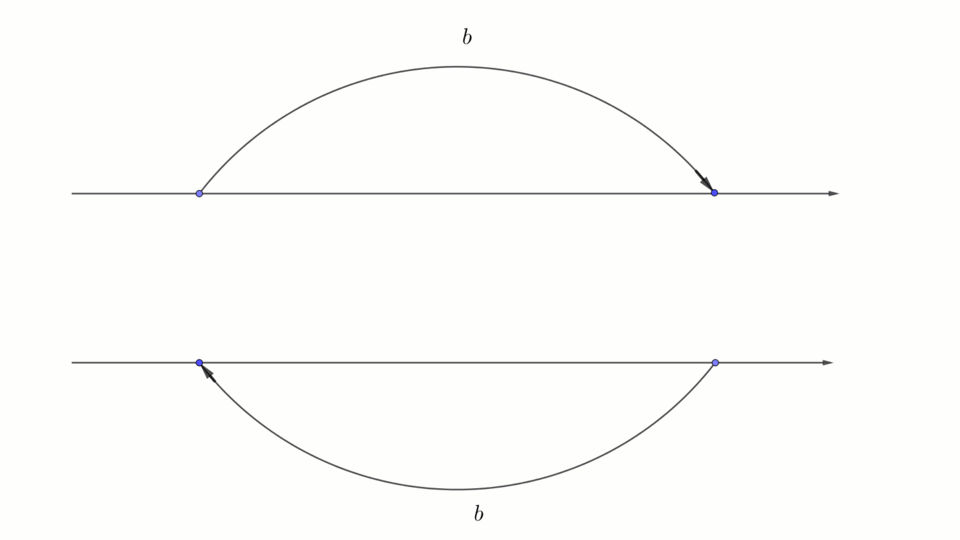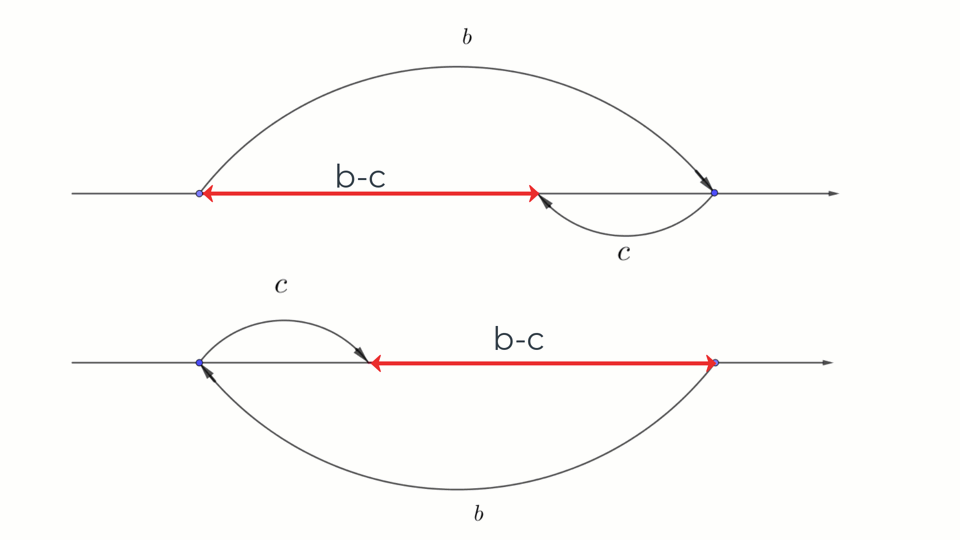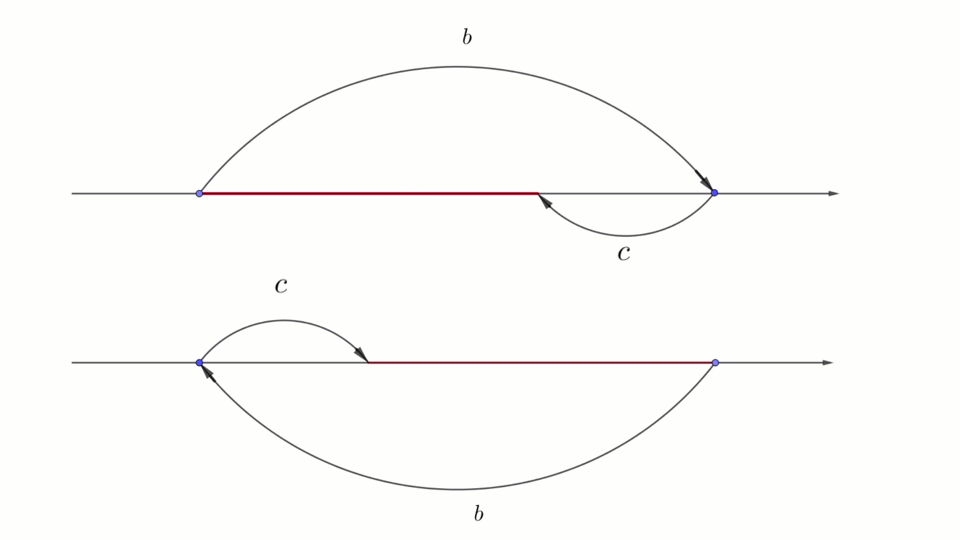

Диаграммада \(\displaystyle a-b+c{\small }\) кесіндісі ұзындығының құрылуы көрсетілген.
\(\displaystyle a-(b-c)=a-b+c\)
 |  | |
| \(\displaystyle a-(b-c)\) | \(\displaystyle =\) | \(\displaystyle a-b+c\) |
Осылайша,кез келген \(\displaystyle a,\, b\) және \(\displaystyle c\) үшін
\(\displaystyle a-(b-c)=a-b+c\) аламыз