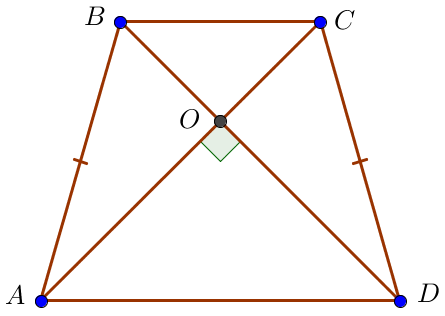
\(\displaystyle ABCD \) трапециясының табандары \(\displaystyle AD \) және \(\displaystyle BC \). \(\displaystyle O \) нүктесі диагональдардың қиылысу нүктесі. \(\displaystyle BD=12\sqrt{2}\small,\) \(\displaystyle OC=5\sqrt{2}\small,\) \(\displaystyle \angle AOD=90^\circ\small.\) \(\displaystyle AD\small\) табу керек.
\(\displaystyle ABD\) және \(\displaystyle ACD\small\) үшбұрыштарын қарастырайық Олар екі қабырғасы мен олардың арасындағы бұрышы арқылы тең:
Сонымен , \(\displaystyle AC=BD=12\sqrt{2}\) және \(\displaystyle \angle ADB=\angle DAC\small.\) | 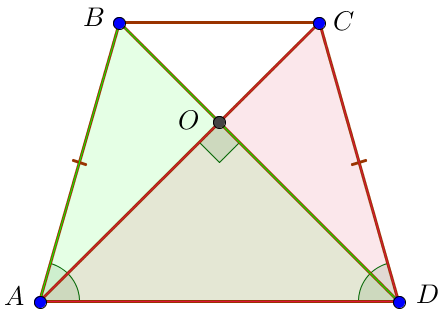 |
Онда
\(\displaystyle AO=AC-OC=12\sqrt{2}-5\sqrt{2}=7\sqrt{2}\small.\)
\(\displaystyle AOD\small\) тікбұрышты үшбұрышын қарастырайық \(\displaystyle \angle OAD = \angle ODA\small,\) онда \(\displaystyle AOD\) үшбұрышы теңбүйірлі, \(\displaystyle AO=OD=7\sqrt{2}\small. \) Пифагор теоремасы бойынша \(\displaystyle AD^2=AO^2 + OD^2=(7\sqrt{2})^2+(7\sqrt{2})^2=\) \(\displaystyle =98+98=196=14^2\small.\) |  |
Кесіндінің ұзындығы оң болғандықтан, онда \(\displaystyle AD=14\small.\)
Жауабы: \(\displaystyle 14{\small .}\)