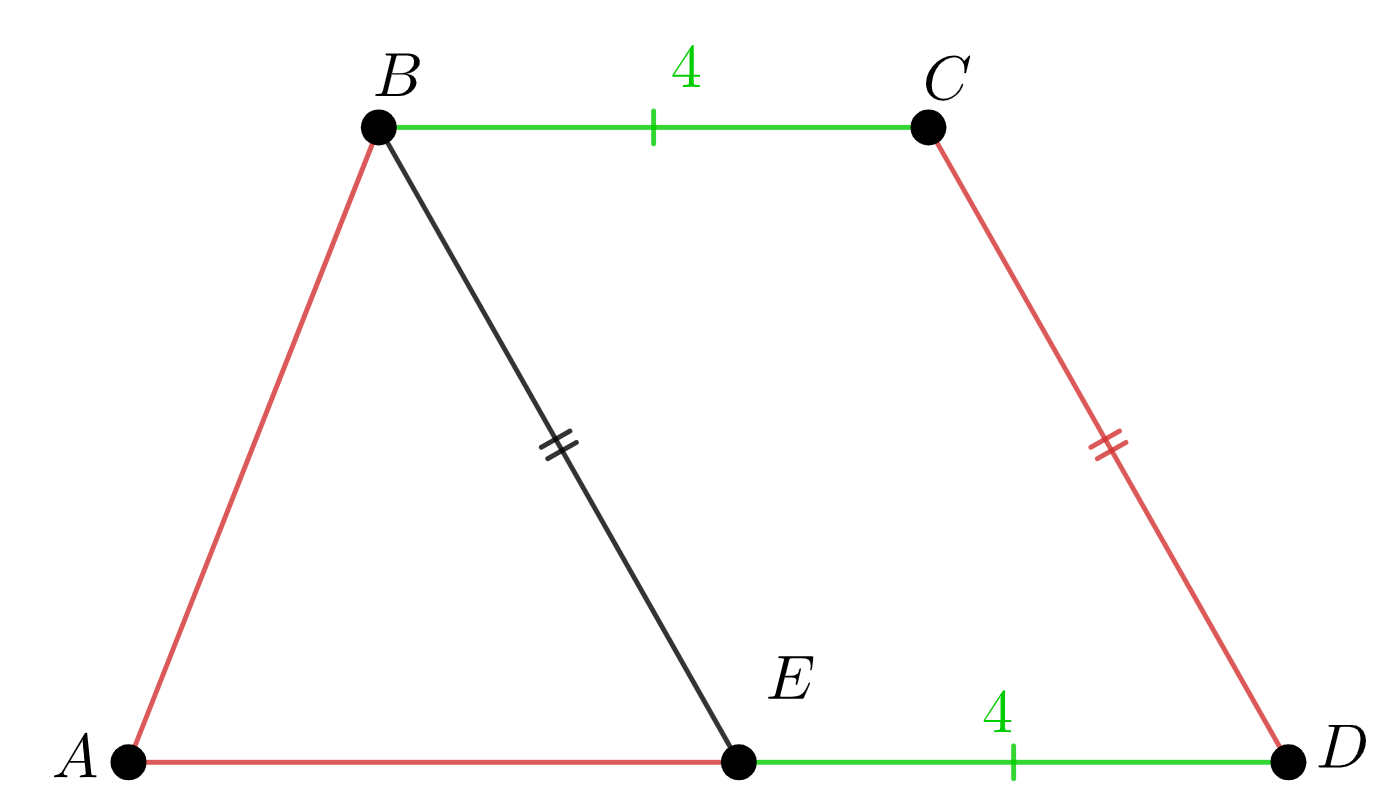
\(\displaystyle ABCD\) трапециясының кіші \(\displaystyle ВС\) табаны \(\displaystyle 4\) тең . \(\displaystyle ВЕ\) түзуі \(\displaystyle CD\) қабырғасына параллель. Егер \(\displaystyle ABE\) үшбұрышының периметрі \(\displaystyle 15\) тең болса, \(\displaystyle ABCD\) трапециясының периметрін табыңыз
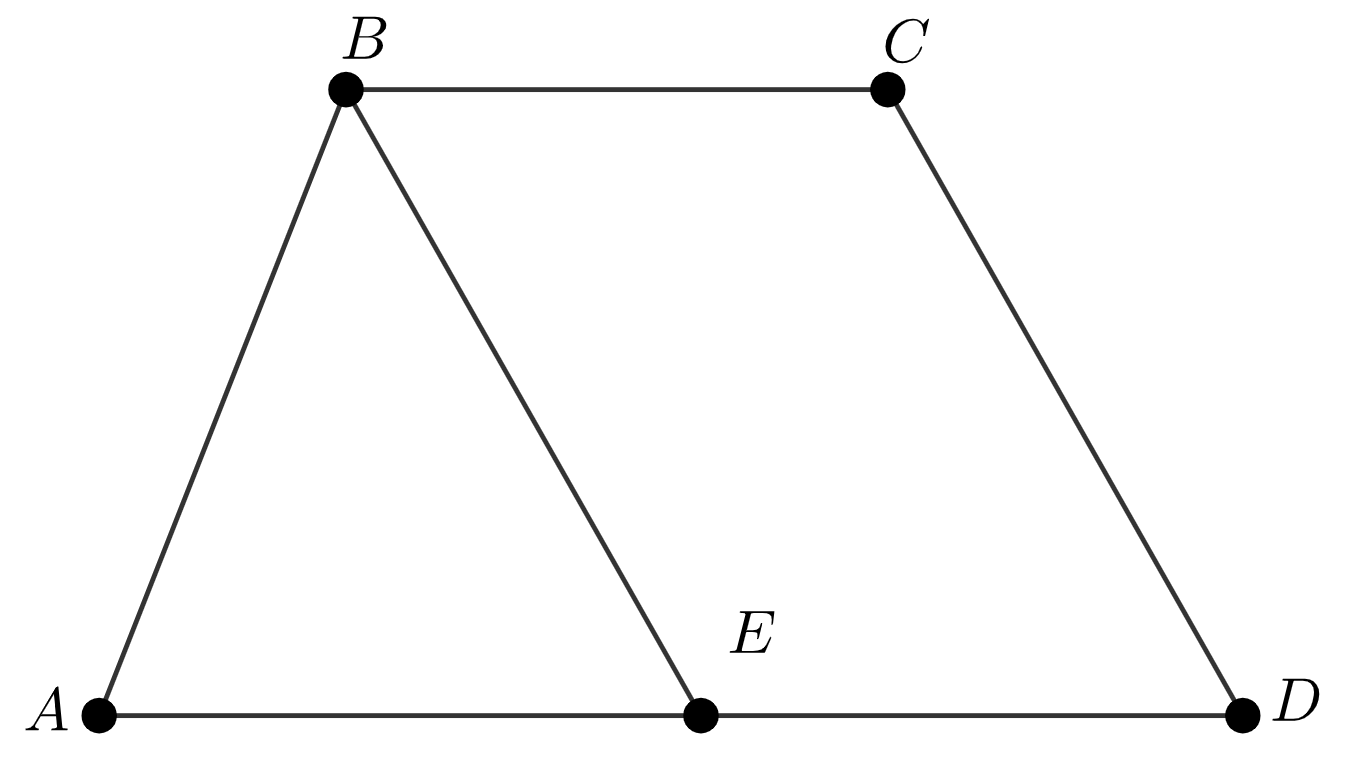
\(\displaystyle BCDE{\small }\) төртбұрышын қарастырайық Онда: Шарт бойынша \(\displaystyle BE\parallel CD\), \(\displaystyle BC\parallel ED\) трапеция негіздері болатын түзулер ретінде. Сонымен , \(\displaystyle BCDE\) – параллелограмм. Сондықтан , \(\displaystyle BC=ED\) және \(\displaystyle BE=CD\small.\) | 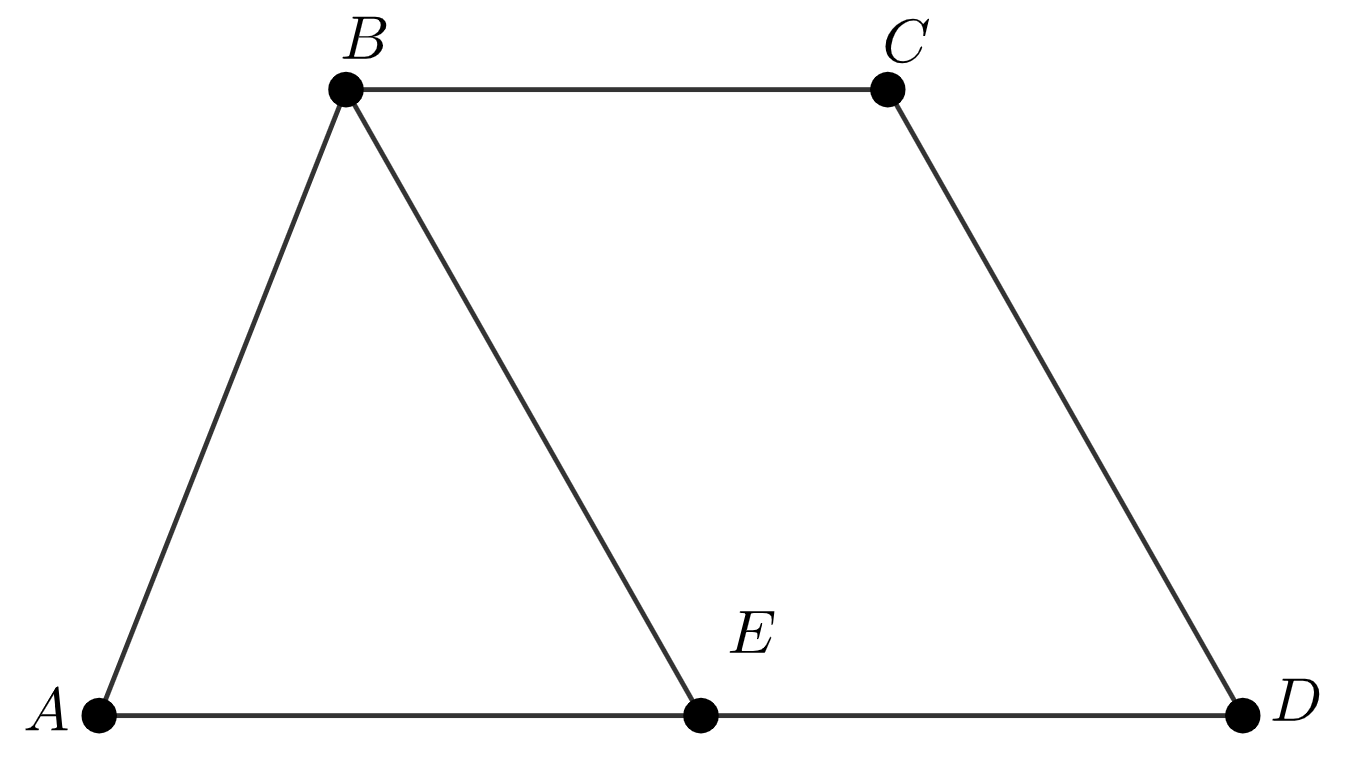 |
\(\displaystyle ABCD{\small }\) трапециясының периметрін табу керек \(\displaystyle P_{ABCD}=AB+BC+CD+DA \small.\) Шарт бойынша \(\displaystyle \color{green}{BC}=\color{green}{ED}=\color{green}{4}\small,\) \(\displaystyle \color{red}{P_{\triangle ABE}}=\color{red}{AB}+\color{red}{BE}+\color{red}{AE}=\color{red}{15}\small.\)
| 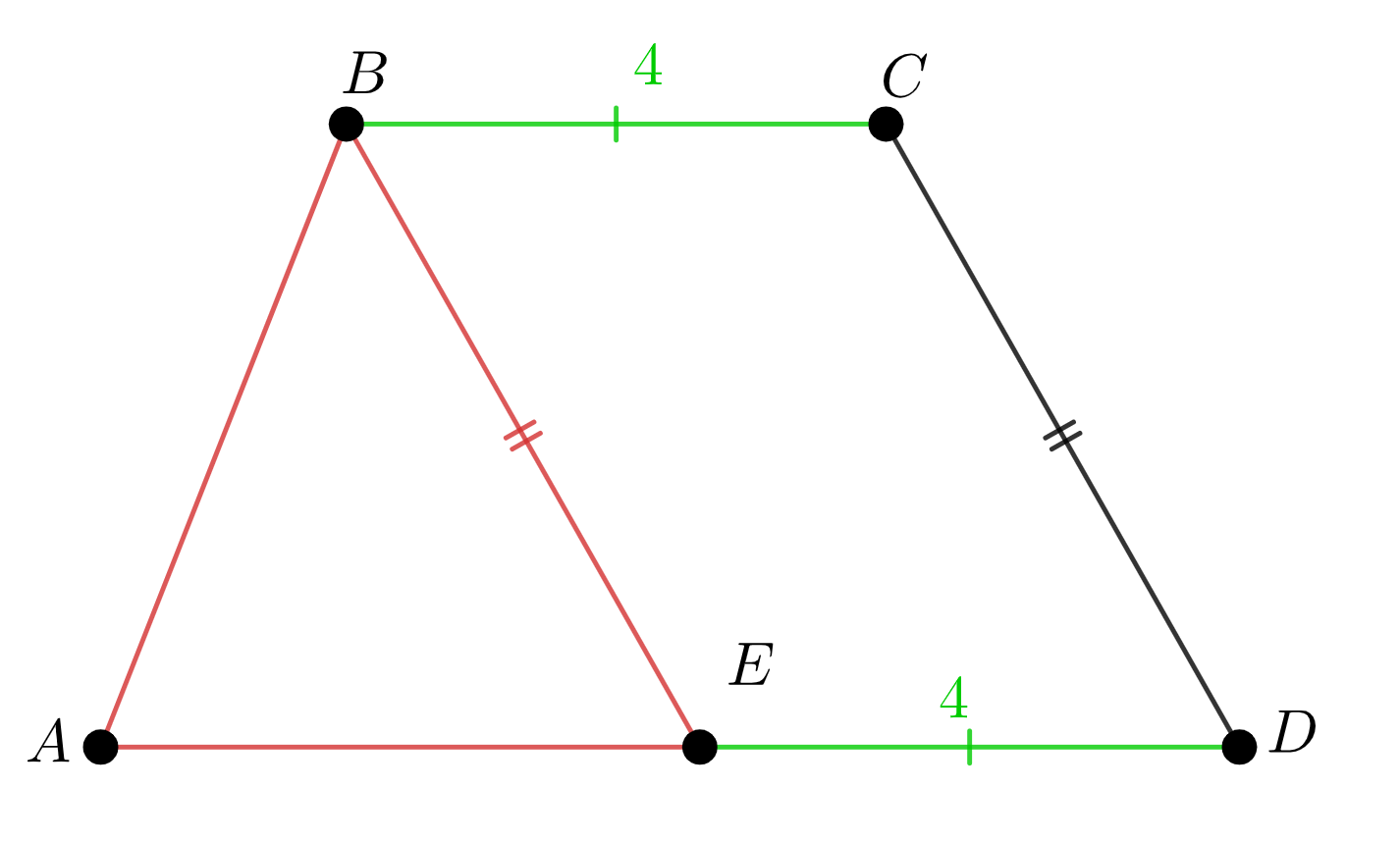 |
\(\displaystyle \color{red}{BE}=\color{red}{CD}\) және \(\displaystyle DA=\color{red}{AE}+\color{green}{ED} \small,\) болғандықтан, онда
\(\displaystyle P_{ABCD}=\color{red}{AB}+\color{green}{BC}+\color{red}{CD}+\color{red}{AE}+\color{green}{ED} \small. \) Яғни \(\displaystyle \begin{aligned} P_{ABCD}&=\color{red}{P_{\triangle ABE}}+\color{green}{BC}+\color{green}{ED}=\\ &=\color{red}{15}+\color{green}{4}+\color{green}{4}=23{\small .} \end{aligned}\) |
|
Жауабы: \(\displaystyle 23{\small .}\)