Трапецияның табандарының кішісі \(\displaystyle 3{\small .}\) Трапецияның диагональдарының орталарын қосатын кесінді \(\displaystyle 2{\small }\)-ге тең. Трапецияның үлкен табанын табыңыз.
\(\displaystyle BC=3\) – \(\displaystyle ABCD{\small }\) трапециясының кіші табаны \(\displaystyle T\) және \(\displaystyle W\) – сәйкесінше
\(\displaystyle AC\) және \(\displaystyle BD\) диагональдарының ортаңғы нүктелері болсын, \(\displaystyle TW=2{\small }\) \(\displaystyle AD{\small }\) табу қажет
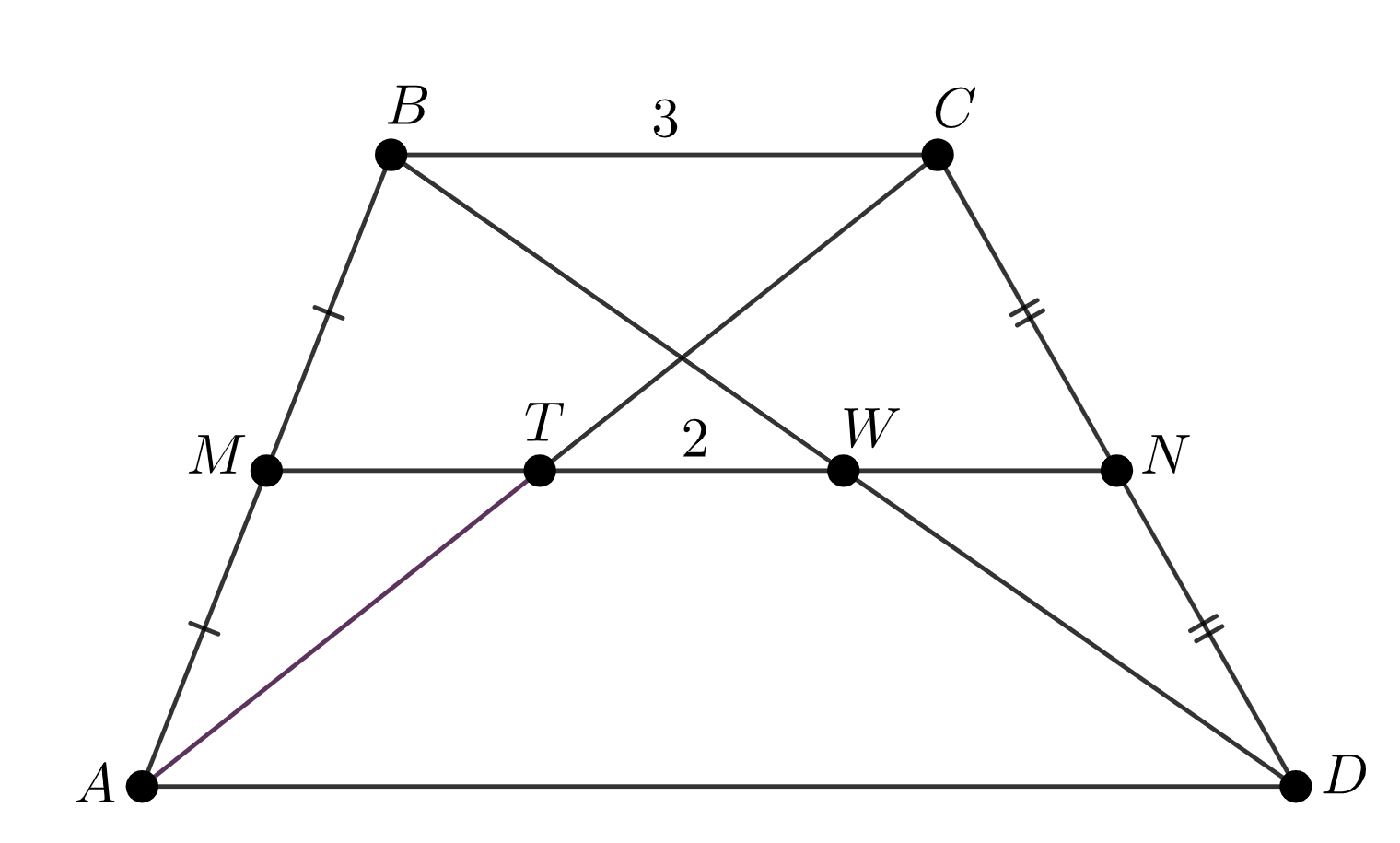
\(\displaystyle M\) және \(\displaystyle N\) – сәйкесінше \(\displaystyle AB\) және \(\displaystyle CD\) жақтарының ортаңғы нүктелері болсын. Трапецияның \(\displaystyle MN\) орта сызығын жүргізейік. Трапецияның орта сызығының қасиеті бойынша \(\displaystyle T\) және \(\displaystyle W\) нүктелері орта сызықта жатады.
|  |
\(\displaystyle MT\) – \(\displaystyle ABC{\small }\) үшбұрышының орта сызығы болғандықтан, онда
\(\displaystyle MT=\frac{BC}{2}=\frac{3}{2}{\small .}\)
\(\displaystyle T\) нүктесі \(\displaystyle MW{\small ,}\) кесіндіде жатқандықтан, онда
\(\displaystyle MW=MT+TW=\frac{3}{2}+2=\frac{7}{2}{\small .}\)
Бірақ \(\displaystyle MW\) – \(\displaystyle ADB{\small }\) үшбұрышының орта сызығы. Демек,
\(\displaystyle MW=\frac{AD}{2}{\small ,}\)
\(\displaystyle AD=2\cdot MW=2\cdot \frac{7}{2}=7{\small .}\)
Жауабы: \(\displaystyle 7{\small .}\)