Трапецияның табандары \(\displaystyle 18 \) және \(\displaystyle 6 \) –ға тең, \(\displaystyle 7 \)-ге тең бүйір қабырғасы трапеция табандарының бірімен \(\displaystyle 150^\circ\small\) бұрыш жасайды . Трапецияның ауданын табыңыз.
\(\displaystyle AD=18\) және \(\displaystyle BC=6\) – табандары, \(\displaystyle AB=7\) – \(\displaystyle ABCD\small\) трапециясының бүйір қабырғасы болсын. Трапецияның ауданын табыңдар.
Трапецияның биіктігін табамыз. Екі нұсқа бар: \(\displaystyle \angle ABC = 150^{\circ}\) және \(\displaystyle \ \angle BAD= 150^{\circ}\small.\)
Есептің тұжырымында ұсынылған фигураға сәйкес, бізде \(\displaystyle \angle ABC = 150^{\circ}\small.\) Трапецияның бүйір жағындағы бұрыштардың қосындысы \(\displaystyle 180^{\circ}\small,\) болғандықтан \(\displaystyle \angle BAD = 180^{\circ}-\angle ABC =\) \(\displaystyle =180^{\circ}-150^{\circ}=30^{\circ}\small.\) Трапецияның \(\displaystyle BH \) биіктігін жүргіземіз. | 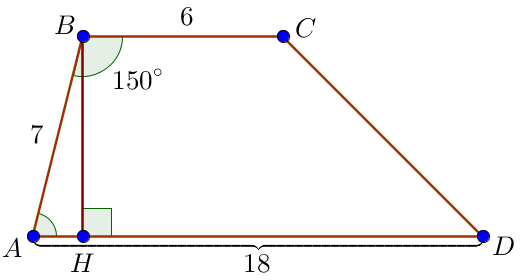 |
\(\displaystyle ABH\small\) тікбұрышты үшбұрышының \(\displaystyle BH \) биіктігін табамыз Бізге \(\displaystyle \angle BAH=30^{\circ}\) сүйір бұрышы және \(\displaystyle AB=7\small\) гипотенузасы белгілі \(\displaystyle 30^{\circ}\small,\) сүйір бұрышы бар тікбұрышты үшбұрыштың қасиеті бойынша \(\displaystyle 30^{\circ}\small,\) бұрышқа қарама-қарсы жатқан катет гипотенузаның жартысына тең. Онда \(\displaystyle BH=\frac{1}{2}\cdot {AB}=\frac{1}{2}\cdot 7=3{,}5\small.\) | 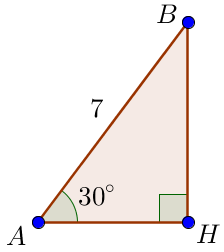 |
Трапецияның ауданы табандарының қосындысының жартысы мен биіктігінің көбейтіндісіне тең болғандықтан, онда
\(\displaystyle S_{ABCD}=\frac{AD+BC}{2}\cdot BH=\frac{18+6}{2}\cdot 3{,}5=\frac{24}{2}\cdot 3{,}5={12}\cdot 3{,}5=42\small.\)
Жауабы: \(\displaystyle 42 \small.\)
\(\displaystyle \angle BAD= 150^{\circ} \small\) жағдайды қарастырайық Трапецияның бүйір жағындағы бұрыштардың қосындысы \(\displaystyle 180^{\circ}\small,\) болғандықтан \(\displaystyle \angle ABC = 180^{\circ}-\angle BAD =\) \(\displaystyle =180^{\circ}-150^{\circ}=30^{\circ} \small.\) Трапецияның \(\displaystyle AH \) биіктігін жүргіземіз. | 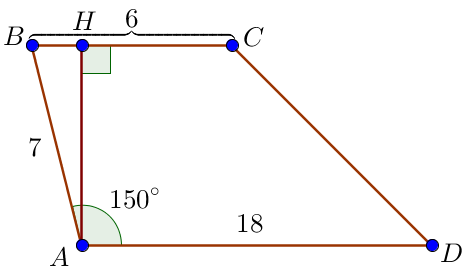 |
Сүйір бұрышы \(\displaystyle \angle ABH =30^{\circ}\) және гипотенузасы \(\displaystyle AB=7 \small\) болатын \(\displaystyle ABH\) тікбұрышты үшбұрышты аламыз. \(\displaystyle 30^{\circ} \small,\) сүйір бұрышы бар тікбұрышты үшбұрыштың қасиеті бойынша\(\displaystyle 30^{\circ} \small,\) бұрышқа қарама-қарсы жатқан катет гипотенузаның жартысына тең. \(\displaystyle AH=\frac{1}{2}\cdot {AB}=\frac{1}{2}\cdot 7=3{,}5 \small.\) Бұл жағдайда трапецияның ауданы \(\displaystyle 42 \small\) тең | 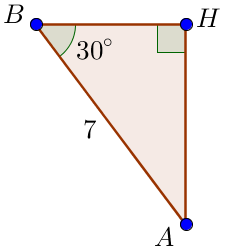 |