Тапсырма
Ромбтың ауданы \(\displaystyle 6\small.\) Оның бір диагональдары екіншісінен \(\displaystyle 3\) есе көп. Кіші диагональді табыңыз.
Шешім
\(\displaystyle BD=x\) – ромбтың кіші диагоналы болсын, онда \(\displaystyle AC=3x \) – ромбтың үлкен диагоналы болсын.
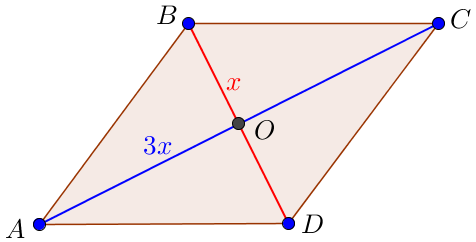
Ромбтың ауданы диагональдардың көбейтіндісінің жартысы болғандықтан
\(\displaystyle S=\frac{1}{2}\cdot AC\cdot BD \small,\)
содан кейін
\(\displaystyle 6 = \frac{1}{2} \cdot 3x\cdot x {\small .}\)
Біз алып жатырмыз:
\(\displaystyle 12 = 3 \cdot x^2{\small,}\)
\(\displaystyle x^2=4{\small .}\)
Кесіндінің ұзындығы оң болғандықтан \(\displaystyle x = \sqrt{4}=2 {\small .}\)
Жауабы: \(\displaystyle 2 {\small .}\)