Үшбұрышта \(\displaystyle ABC\) бұрыш \(\displaystyle \angle A\) тең \(\displaystyle 60^\circ{\small , }\) бұрыш \(\displaystyle \angle B\) тең \(\displaystyle 82^\circ{\small , }\) \(\displaystyle AD{\small,}\) \(\displaystyle BE\) және \(\displaystyle CF\) – \(\displaystyle O{\small }\) нүктесінде қиылысатын биссектрисалар. Бұрышты \(\displaystyle AOF{\small }\) табыңыз
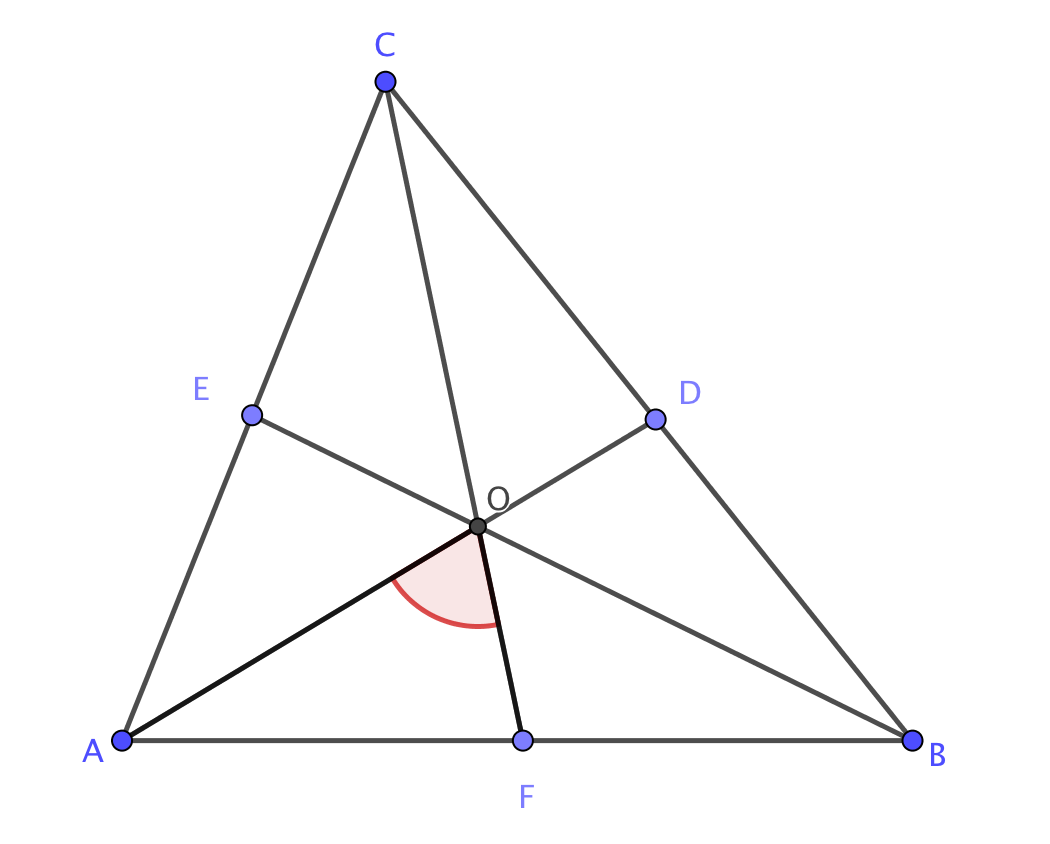
Шарт бойынша бұрышты \(\displaystyle AOF{\small } \) табыңыз
Себебі бұрыштардың қосындысы үшбұрышта \(\displaystyle 180^\circ{\small ,} \) тең онда үшбұрышта \(\displaystyle ABC \) бұрыш \(\displaystyle C \) тең
\(\displaystyle \angle C=180-\angle A- \angle B= 180^\circ- 60^\circ- 82^\circ= 38^\circ{\small . } \)
Егер \(\displaystyle x \) градус болса, онда бұрыш \(\displaystyle AOF{\small . } \) Себебі \(\displaystyle AD{\small,}\) \(\displaystyle DE\) және \(\displaystyle CF\) – биссектрисалар, содан кейін біз бұрыштардың келесі мәндерін аламыз:
\(\displaystyle \angle AOF=x \) – үшбұрыштың \(\displaystyle AOC{\small} \) сыртқы бұрышы. Себебі сыртқы бұрыш үшбұрыштың оған іргелес емес екі бұрыштың қосындысына тең, онда
\(\displaystyle x=30^{\circ}+19^{\circ}=49^{\circ}{\small. }\)
Жауап: \(\displaystyle 49 {\small .} \)