Тікбұрышты үшбұрышта \(\displaystyle ABC\) тік бұрыштың жоғарғы жағынан сызылған биссектриса \(\displaystyle CD\) мен медиана \(\displaystyle CM{\small , }\) арасында бұрыш тең \(\displaystyle 14^\circ{\small .}\) Тікбұрышты үшбұрыштың \(\displaystyle ABC{\small }\) сүйір бұрыштардың үлкенін табыңыз.
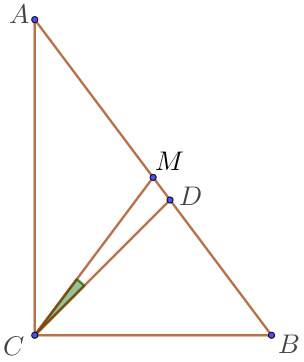
Себебі гипотенузаға жүргізілген медиана гипотенузаның жартысына тең, үшбұрыш және \(\displaystyle AMC \) және \(\displaystyle CMB \) – теңбүйірлі.
Егер \(\displaystyle \angle B= \alpha{\small .} \) Себебі \(\displaystyle \triangle CMB \) – теңбүйірлі, онда \(\displaystyle \angle MCB= \angle B= \alpha{\small :} \)
Себебі \(\displaystyle CD \) – биссектриса, онда \(\displaystyle \angle BCD= 45^\circ{\small .} \)
Жалпы:
Онда
\(\displaystyle \angle MCB= \angle MCD+ \angle DCB{\small , } \)
\(\displaystyle \alpha= 14^\circ+ 45^\circ{\small , } \)
\(\displaystyle \alpha= 59^\circ{\small , } \)
\(\displaystyle \angle B= 59^\circ{\small . } \)
Себебі \(\displaystyle \angle A+ \angle B= 90^\circ{\small , } \) онда \(\displaystyle \angle A= 90^\circ- 59^\circ= 21^\circ{\small .} \)
Ең үлкен сүйір бұрыш \(\displaystyle 59^\circ{\small } \) тең.
Жауап: \(\displaystyle 59 {\small .} \)