Тікбұрышты үшбұрышта \(\displaystyle ABC\) тік бұрыштың жоғарғы жағынан алынған биіктік \(\displaystyle CH\) мен медиана \(\displaystyle CM{\small , }\) арасында бұрыш тең \(\displaystyle 40^\circ{\small .}\) Тікбұрышты үшбұрыштың \(\displaystyle ABC \) сүйір бұрыштардың үлкенін табыңыз.
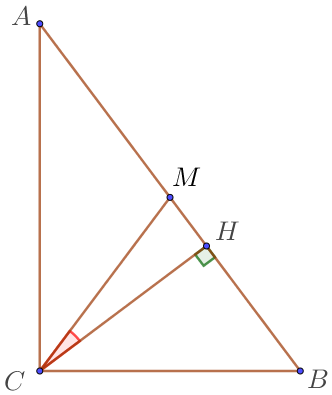
Тікбұрышты үшбұрышта гипотенузаға жүргізілген медиана гипотенузаның жартысына тең.
Сондықтан \(\displaystyle CM= AM= MB{\small .} \)
\(\displaystyle \alpha{\small } \) арқылы \(\displaystyle B \) бұрышты белгілейміз. Себебі \(\displaystyle \triangle CHB \) – тікбұрышты, онда \(\displaystyle \angle HCB= 90^\circ- \alpha{\small .} \)
\(\displaystyle \angle C= 90^\circ \) және \(\displaystyle \angle C= \angle ACM+ \angle MCH+ \angle HCB{\small , } \)
\(\displaystyle 90^\circ= \angle ACM+ 40^\circ+ 90^\circ- \alpha{\small , } \)
\(\displaystyle \angle ACM= \alpha- 40^\circ{\small .} \)
\(\displaystyle \triangle ACM \) – теңбүйірлі. Демек, \(\displaystyle \angle A= \angle MCA= \alpha- 40^\circ{\small .} \)
\(\displaystyle \angle B= \alpha \) және \(\displaystyle \angle A= \alpha- 40^\circ{\small } \) аламыз
Себебі \(\displaystyle \angle B+ \angle A= 90^\circ{\small , } \) онда аламыз:
\(\displaystyle \alpha+ \alpha- 40^\circ= 90^\circ{\small ,} \)
\(\displaystyle 2\alpha= 90^\circ+ 40^\circ {\small , }\)
\(\displaystyle 2\alpha= 130^\circ {\small , }\)
\(\displaystyle \alpha= 65^\circ {\small . }\)
Осылайша,
\(\displaystyle \angle B= 65^\circ{\small , } \)
\(\displaystyle \angle A= 90^\circ-65^\circ= 25^\circ{\small .} \)
Үлкен бұрыш \(\displaystyle 65^\circ{\small } \) тең
Жауап: \(\displaystyle 65 {\small .} \)