Дұрыс үшбұрышты пирамида табанының қырларын \(\displaystyle 16 \) бүйір бетінің ауданы \(\displaystyle 360 \) тең. Осы пирамиданың бүйір қабырғалары табыңдар.
Есептің шартына сәйкес табан қыры \(\displaystyle BC=16\) және бүйір бетінің ауданы \(\displaystyle S_{бүй}=360 {\small }\) берілген
Пирамиданың бүйір қабырғасын \(\displaystyle SC{\small }\) табу қажет.
Дұрыс пирамиданың бүйір жақтары – тең үшбұрыштар. Демек, бүйір жақтарының аудандары тең.
Дұрыс үшбұрышты пирамиданың үш бүйір жағы бар. Яғни,
\(\displaystyle S_{бүй}=S_{жақт}+S_{жақт}+S_{жақт}=3S_{жақт}\small. \)
Содан кейін
\(\displaystyle 360=3S_{жақт}\small, \)
\(\displaystyle S_{жақт}=120\small. \)
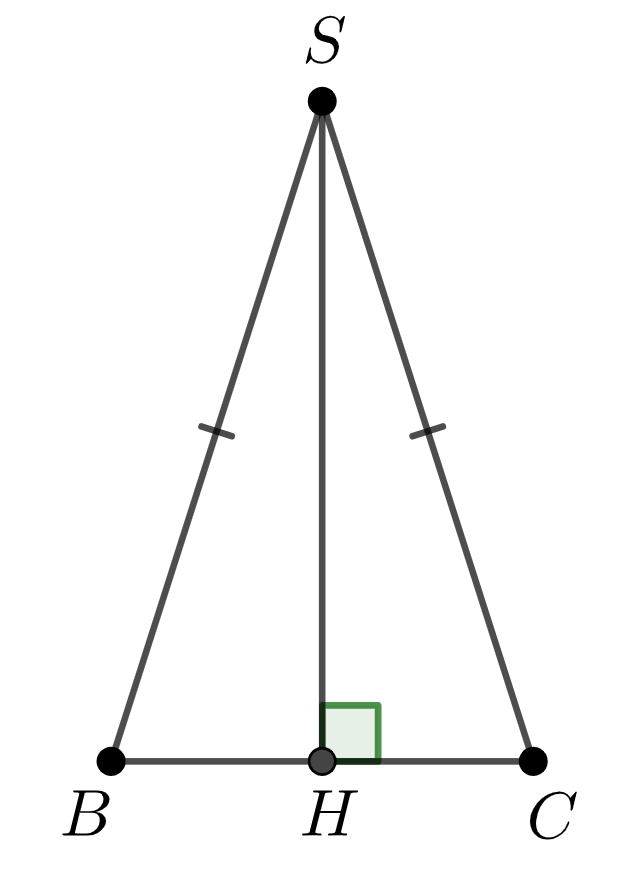
\(\displaystyle SBC{\small }\)жағына \(\displaystyle SH\) биіктігін жүргізейік
|
|
Үшбұрыштың ауданы қабырға мен оған түсірілген биіктіктің көбейтіндісінің жартысына тең. Яғни
\(\displaystyle S_{жақт}=\frac{1}{2}BC\cdot SH{\small .}\)
\(\displaystyle SH{\small }\) табайық
\(\displaystyle 120=\frac{1}{2}\cdot 16 \cdot SH{\small ,}\)
\(\displaystyle 120=8 \cdot SH{\small ,}\)
\(\displaystyle SH=15{\small .}\)
\(\displaystyle SH\) кесіндісі тең қабырғалы \(\displaystyle SBC{\small }\) үшбұрышының \(\displaystyle BC{\small} \) табанына жүргізілген биіктік болып табылады.
Демек, \(\displaystyle SH\) сонымен қатар \(\displaystyle SBC{\small }\) үшбұрышының медианасы болып табылады.
Яғни,
\(\displaystyle BH=HC=\frac{1}{2}BC=\frac{1}{2}\cdot 16 = 8{\small .}\)
Тік бұрышты \(\displaystyle SHC{\small }\) үшбұрышын қарастырайық
\(\displaystyle SHC{\small }\) үшбұрышы үшін Пифагор теоремасы бойынша \(\displaystyle SC{\small }\) табайық \(\displaystyle SH^2+HC^2=SC^2{\small ,}\) \(\displaystyle SC^2=15^2+{17}^2{\small ,}\) \(\displaystyle SC^2=289{\small .}\) \(\displaystyle SC{\small }\) кесіндінің ұзындығы болғандықтан, онда \(\displaystyle SC>0\) демек, \(\displaystyle SC=\sqrt{289}=17{\small .}\) |
Жауабы: \(\displaystyle 17{\small .}\)