Skip to main content

Теориясы: 08 Пирамида бетінің ауданы

Тапсырма

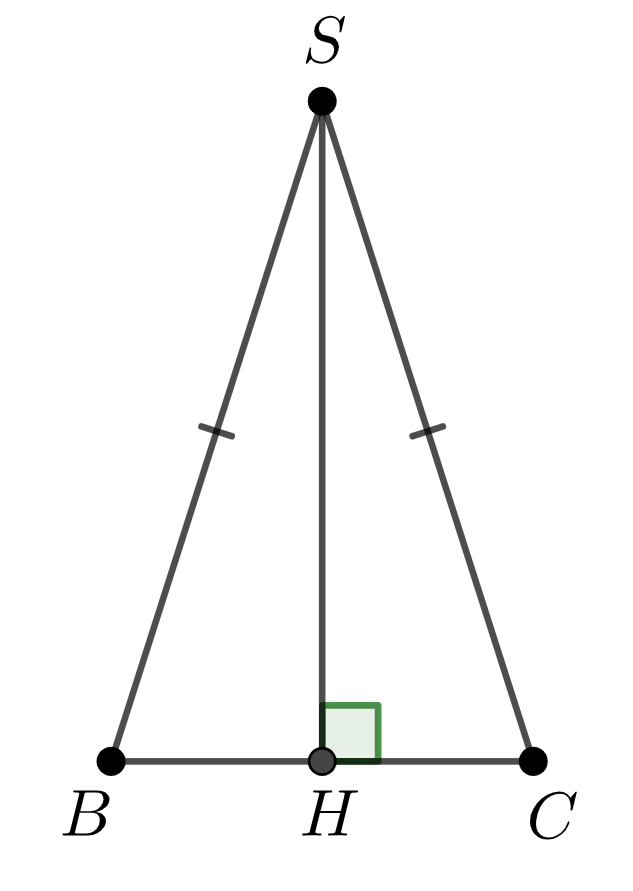
Дұрыс төртбұрышты пирамида табанының қырлары \(\displaystyle 10 , \) бетінің ауданы \(\displaystyle 340 \) тең. Осы пирамиданың бүйір қабырғасын табыңыз.

Шешім

Есептің шарты бойынша табан қыры \(\displaystyle BC=10\) және бетінің ауданы \(\displaystyle S=340 {\small }\) тең.

Пирамиданың бүйір қабырғасын \(\displaystyle SC{\small }\) табу қажет.

Ол үшін  \(\displaystyle SBC{\small }\) бүйір жағын қарастырайық.

Шарттан \(\displaystyle SBC{\small }\) жағында \(\displaystyle BC{\small} \) қабырғасы белгілі

Шартта бетінің ауданы берілгенін пайдаланып \(\displaystyle SH{\small ,}\) апофемасын табуға болады.

Содан кейін  \(\displaystyle HC=\frac{1}{2}BC{\small}\) болғандықтан,  \(\displaystyle SHC{\small }\) үшбұрышы үшін Пифагор теоремасы бойынша  \(\displaystyle SC\) 

I.  \(\displaystyle SH{\small }\) апофемасын табайық

Есептің шартында пирамиданың бетінің ауданы берілген. 

Пирамиданың толық бетінің ауданын есептеу үшін формуланы қолданайық.

Правило

Пирамиданың толық беті

Пирамиданың толық бетінің ауданы \(\displaystyle S\) келесіге тең.

\(\displaystyle S=S_{табан}+S_{бүй} { \small ,} \)

мұндағы \(\displaystyle S_{табан} \) – табан ауданы,

\(\displaystyle S_{ бүй }\)  - пирамиданың бүйір бетінің ауданы.

Бұл ретте:

  • ауданы \(\displaystyle S\) белгілі;
  • табан ауданы \(\displaystyle S_{табан}\) табанында шаршы жататындықтан, табан жағы арқылы есептеледі;
  • бүйір бетінің ауданы \(\displaystyle S_{бүй}\) апофема мен табан қабырғасы арқылы есептеледі..

 \(\displaystyle SH\) табу үшін келесі қажет:

1. \(\displaystyle S_{табан}{\small }\) есептеу

2.  \(\displaystyle S_{бүй}=4S_{жақт}\) және \(\displaystyle S_{жақт}=\frac{1}{2}\cdot BC \cdot SH{ \small }\)  пайдаланып \(\displaystyle SH{\small }\) арқылы  \(\displaystyle S_{бүй}\) өрнектеу

3.  \(\displaystyle S\small \)  арналған формулаға \(\displaystyle S_{табан}\) және \(\displaystyle S_{бүй}\) алмастыру арқылы   \(\displaystyle SH{\small }\) табу.

 

1. Пирамида табанының ауданын табайық.

\(\displaystyle S_{табан}=100 \)

2. Бүйір бетінің \(\displaystyle S_{ бүй }\)  ауданын \(\displaystyle SH{\small }\) апофемасы арқылы өрнектейміз.

\(\displaystyle S_{бүй}=4S_{жақт}=20\cdot SH \)

3. \(\displaystyle SH{\small }\) табайық

\(\displaystyle SH=12 \)

II. Бүйір қабырғасын \(\displaystyle SC{\small }\)  табыңыз

\(\displaystyle SBC{\small }\) бүйір жағын қарастырыңыз

\(\displaystyle SH\) апофемасы \(\displaystyle BC\)табанына жүргізілген тең қабырғалы \(\displaystyle SBC{\small }\) үшбұрышының биіктігі болып табылады.

Демек, \(\displaystyle SH\) сонымен қатар  \(\displaystyle SBC{\small }\) үшбұрышының медианасы болып табылады.

Яғни,

\(\displaystyle BH=HC=\frac{1}{2}BC=\frac{1}{2}\cdot 10 = 5{\small .}\)

Тік бұрышты \(\displaystyle SHC{\small }\)  үшбұрышын қарастырайық

\(\displaystyle SHC{\small }\)  үшбұрышы үшін Пифагор теоремасын пайдаланып \(\displaystyle SC{\small }\) табайық

\(\displaystyle SH^2+HC^2=SC^2{\small ,}\)

\(\displaystyle 12^2+5^2=SC^2{\small ,}\)

\(\displaystyle SC^2=169{\small .}\)

Кесіндінің ұзындығы оң болғандықтан, онда 

\(\displaystyle SC=\sqrt{169}=13{\small .}\)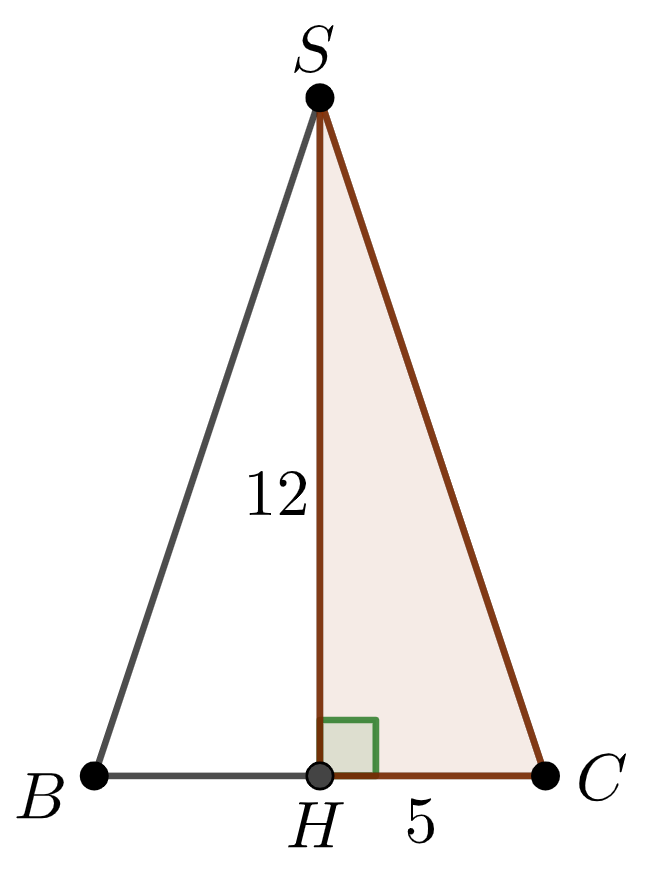

Жауабы: \(\displaystyle 13{\small .}\)