Дұрыс төртбұрышты пирамида табанының қабырғасы \(\displaystyle 4 , \) ал пирамиданың бетінің ауданы \(\displaystyle 64 \) тең. Апофемасын табыңыз.
Анықтаманы қолданайық.
Дұрыс пирамиданың апофемасы
Дұрыс пирамиданың төбесінен жүргізілген бүйір жағының биіктігі апофема деп аталады.
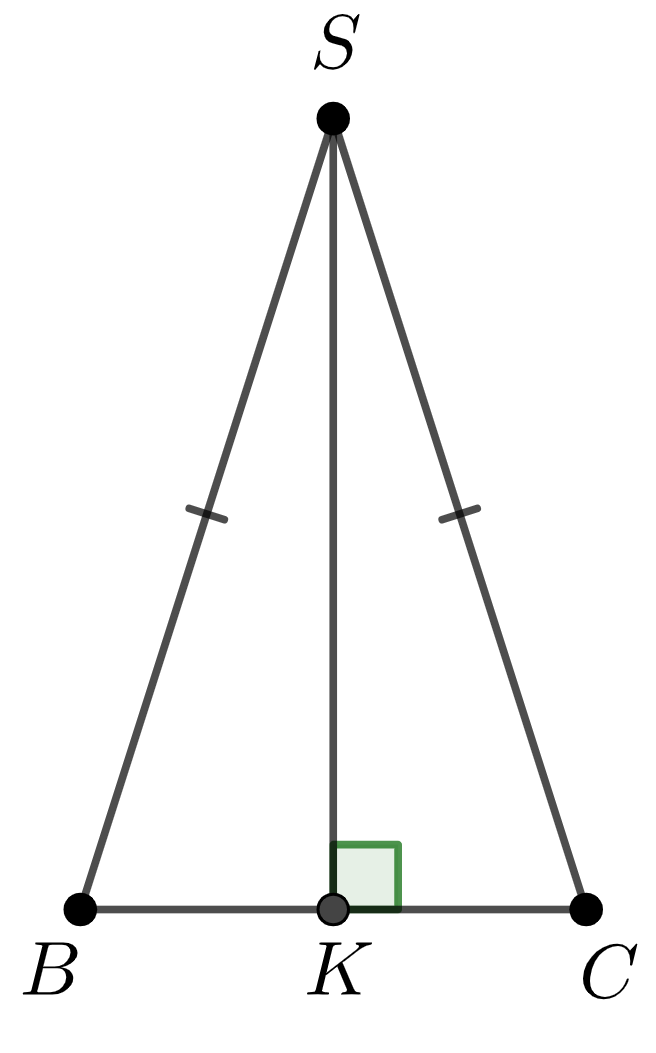
Сонда \(\displaystyle SK\) осы пирамиданың апофемасы болып табылады.
Дұрыс үшбұрышты пирамиданың табан жағы \(\displaystyle BC=4\) – болсын.
Пирамиданың толық бетінің ауданын есептеу үшін формуланы қолданайық.
Пирамиданың толық беті
Пирамиданың толық бетінің ауданы \(\displaystyle S\) келесіге тең.
\(\displaystyle S=S_{табан}+S_{бүй} { \small ,} \)
мұндағы \(\displaystyle S_{табан} \) – табан ауданы,
\(\displaystyle S_{ бүй }\) - пирамиданың бүйір бетінің ауданы.
Пирамиданың толық бетінің ауданы үшін формулаға \(\displaystyle S_{табан}\)және \(\displaystyle S_{ бүй }\) қояйық:
\(\displaystyle S=S_{табан}+S_{бүй} {\small ,}\)
\(\displaystyle S=16+8\cdot SK {\small .}\)
\(\displaystyle S\) алмастырып, пирамиданың \(\displaystyle SK{\small }\) апофемасын есептейік:
\(\displaystyle 64=16+8\cdot SK{ \small ,} \)
\(\displaystyle 8\cdot SK=48{ \small ,}\)
\(\displaystyle SK=6{ \small .}\)
Жауабы: \(\displaystyle 6{\small .}\)